[서울대 물리학실험 1-1] 뉴턴의 사과는 어떻게 떨어졌는가? / 포물선 운동

물리학 실험 1-1

1-1A. 뉴턴의 사과는 어떻게 떨어졌는가?

1-1B. 포물선 운동

1. Introduction

1.1. 실험 목적

1.1.1. 실험 1-1A : 지구 상의 물체는 자연계에 기본적으로 존재하는 4가지 힘 중 하나인 중력에 의해 지구 중심 방향으로
힘을 받게 된다. 실험실의 관측자에게는 이것이 지면으로 낙하하는 것처럼 보이는데, 이 운동을 분석하여 어떠한 물리량에
일정한 규칙이 나타나는지 확인해본다.

1.1.2 실험 1-1B : 포물체 운동은 2차원 평면 상의 등속도 운동과 수직 방향의 등가속도 운동이 결합되어 나타나는데,
이러한 것들을 실험을 통해 확인해본다.

1.2. 배경 지식

1.2.1 뉴턴의 제2법칙

힘은 물체의 운동 상태를 변화시킬 수 있는 요인이 된다. 이 운동 상태의 변화는 가속도로 나타난다. 이를 식으로 나타내면,

힘이 일정한 등가속도 운동의 경우,

1.2.2 중력가속도

뉴턴이 발견한 중력에 대한 식은 다음과 같다.

물체가 움직이는 거리가 지구 반지름에 비해 매우 작은 경우, 위 공식의 대신 지구 반지름 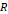을 대입할 수 있으며,
이렇게 보면 자유낙하 운동은 등가속도 운동처럼 보이게 된다. 이때, 그 가속도를 중력가속도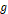 (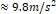)라
한다.

1.2.3 마찰력

공기 중에서 낙하하는 물체는 공기의 마찰력을 받게 되어 있다.

1.2.4 부력

부력이란 유체의 압력 차에 의해 생겨나는 힘을 말한다. 대기압이 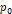일 때, 깊이가 인 지점에서 밀도가 인 유체가
받는 압력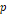 는

또, 부피가 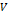인 물체가 유체 속에서 받는 부력은

1.2.5 마찰 없는 포물선 운동

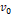중력이 방향으로 작용하는 좌표계에서, 초기속도 으로 x축에서 양의 방향으로 각 θ만큼 기울어진 채 발사된
물체가 있다고 하자. 시간 t에 따른 물체의 좌표를 (x(t), y(t)) 라고 하면,

이 두 식을 정리하면 다음과 같이 나온다.

낙하해서 착지까지 걸리는 시간 T에 대해

또, 최대 수평 방향 이동 에 대해서

1.2.6 마찰이 있는 포물선 운동

일반적으로 속력이 v인 물체는 다음과 같은 마찰력을 받는다.

간단히, 마찰력이 속도에 비례한다 가정하면,

이를 통해 다음과 같은 식을 할 수 있다.

또 속도에 관해서는,

축에 대한 속도는 시간이 충분한 지난 뒤에 종단 속도 (-)에 도달한다는 것을 알 수 있다.

1.3. 실험 안내

1.3.1 실험 1-1A 중 실험 1

정확도가 인간에 비해 높은 CCD 카메라를 이용해서 실험을 진행하도록 한다.

먼저, CCD 카메라를 흰색 스크린 앞에 세운다. 그리고 테이프를 붙인 플라스틱 막대를 카메라와 스크린 사이의 탁상 위에
세운다. 카메라와 연결된 컴퓨터에 설치된 I-CA 프로그램을 이용해, 카메라의 초점이나 밝기 설정과 좌표계 설정을 한다.
이때, 줌이 4 이하가 되도록 한다.

플라스틱 막대의 테이프 중 위에 있는 테이프의 높이에서 밝은 색을 띠는 구슬을 떨어뜨리고, 그 모습을 카메라를 이용해
캡처한다. 캡처한 자료를 프로그램을 이용해서 분석하도록 한다. 이 과정을 적어도 3번은 반복한다.

1.3.2 실험 1-1A 중 실험 2

실험 1-1A 중 1을 진행했던 환경 그대로에서 실험을 진행하도록 한다. 우선, 구슬 하나에는 공기를 넣은 풍선을 매달고,
다른 구슬 하나에는 헬륨을 넣은 풍선을 매단다. 그리고 각각 하나씩 실험 1을 진행했던 과정 그대로 실험을 해 본다.
이 과정을 추 하나당 2번 정도 반복한다.

1.3.3 실험 1-1B 중 실험 1

먼저, 발사대를 흰색 스크린 앞에 설치한다. 발사체가 어디까지 날아갈 지 예상하고, 발사체 착지 예상 지점과 발사대의
중간 지점에 CCD 카메라를 설치한다. 카메라 좌표계 설정을 진행하고, 눈에 잘 띠는 색의 구슬을 발사대에 넣는다.
첫 번째로는 발사대를 30도 기울여서 발사하고, 다음에는 45도, 그 다음에는 60도 기울여서 발사하는데, 각각의 각도마다
2번씩은 실험한다. 발사체가 발사되는 모습을 카메라로 캡처하고, 캡처한 자료를 프로그램을 통해 분석한다.

1.3.4 실험 1-1B 중 실험 2

실험 1-1B 중 1을 진행한 환경 그대로에서 실험을 진행하도록 한다. 실험 1에서 사용한 구슬의 질량을 재고, 또 이와는
다른 질량을 가진 구슬을 가져와서 무게를 잰 뒤, 45도로 기울어진 발사대에서 발사하도록 한다. 발사되는 장면을 카메라
로 캡처하고, 캡처한 자료를 프로그램을 이용하여 분석하도록 한다.

2. Data & Result

2.1. 1-1A의 실험 결과

2.1.1 실험 1-1A 중 실험 1의 결과

구슬의 자유낙하 운동을 지켜보는 실험을 3번 진행하였다. 우선, 시간에 대한 구슬의 높이가 어떤 패턴을 보이는지 보았다.
다음은 시간-구슬의 높이에 대한 그래프이다.

그림 1: 자유낙하 운동의 시간-높이 그래프

실험 1,2,3 모두 그래프가 포물선을 그리고 있음을 확인할 수 있다. 몇몇 값을 그래프에서 제외하면, 그래프의 형태도 모두
평행이동한 것처럼 비교적 비슷해 보인다. ‘이론’ 그래프는 9.8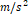의 가속도로 낙하하는 물체에 대한 그래프이다.

각각의 시도에 대한 중력가속도 값을 구해보는데, 그 구하는 방법을 두 가지로 잡았다.

첫 번째 방법은, 각 프레임들의 사이에서 일어난 운동 각각의 평균 가속도를 구하는 방법이었다.
또, 두 번째 방법은, 각 프레임마다 처음부터 지금의 프레임까지 일어난 운동의 평균 가속도를 구하는 방법이었다.
아래는 두 방법의 결과이다. 단, 추의 초기속도는 0이라고 보았다.

	평균 가속도의 평균(㎨)	표준편차
1	11.498	10.281
2	9.475	7.251
3	8.252	3.920
전체	9.742

표 1: 첫 번째 방법으로 산출한 표

표 1은 첫 번째 방법으로 산출한 표이다. 평균이 9.742로 이론값인 9.8에 매우 근접하나, 각각 실험에서 구한 자료들의
표준편차가 매우 심한 것을 확인할 수 있다. 이는 첫 번째 방법으로 산출하면  카메라 캡처 기능의 한계로 인한 오차 발생을
제거하기가 매우 까다롭기 때문이었다.

	평균 가속도의 평균(㎨)	표준편차
1	9.615	1.673
2	9.493	1.889
3	9.090	1.279
전체	9.399

표 2: 두 번째 방법으로 산출한 표

표 2는 두 번째 방법으로 산출한 표이다. 두 번째 방법으로 산출한 자료는 오차가 비정상적인 값을 제거하는 것이
가능했기 때문에 표준편차를 줄일 수 있었다.

2.1.2 실험 1-1A 중 실험 2의 결과

시간에 따른 구슬의 높이가 어떻게 변하는지 실험 1의 결과와 비교해보면 그림 2와 같다. 풍선이 달려있지 않은 구슬의
낙하 운동이 진공 상태에서 떨어지는 구슬의 낙하 운동과 같은 형태를 띨 것이라고 가정한 뒤 그래프를 그렸다.

그림 2: 여러 추들의 낙하운동 비교

풍선이 달린 구슬들이 풍선이 없는 구슬보다 더 빨리 떨어지는 것을 확인할 수 있다. 또, 공기가 들어있는 풍선에 매달린
구슬과 헬륨이 들어있는 풍선에 매달린 구슬의 낙하를 비교해 보았을 때, 공기가 들어있는 풍선에 매달린 구슬의 가속도를
2.1.1에서 제시한 첫 번째 방법과 두 번째 방법으로 각각 구해 보았다.

	평균 가속도의 평균(㎨)	표준편차
방법 1	8.027	0.954
방법 2	8.398	0.690

표 3: 공기가 든 풍선이 달린 추의 가속도

또, 비교해서 헬륨이 들어있는 풍선에 매달린 구슬의 가속도를 첫 번째 방법으로 분석해 보면,

	평균 가속도의 평균(㎨)	표준편차
1	6.373	0.539
2	6.229	0.556
전체	6.301

표 4: 첫 번째 방법으로 산출한 표

다음에는 두 번째 방법으로 분석해 보면,

	평균 가속도의 평균(㎨)	표준편차
1	7.078	0.675
2	6.902	2.157
전체	6.990

표 5: 두 번째 방법으로 산출한 표

공기가 든 풍선에 달린 구슬의 가속도에 비해 헬륨이 든 풍선에 달린 구슬의 가속도가 작음을 알 수 있다.

2.2. 1-1B의 실험 결과

2.2.1 1-1B 중 실험 1의 결과

발사체의 운동을 세 가지 그래프로 나타낼 수 있으며, 이는 아래의 그림과 같다.

그림 3: 다각도로 쏜 구슬의 시간에 따른 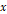좌표

그림 4: 다각도로 쏜 구슬의 시간에 따른 좌표

그림 5: 다각도로 쏜 구슬의 궤적

2.2.2 1-1B 중 실험 2의 결과

7.5g짜리 구슬 G와 6.0g짜리 구슬 R을 이용해서 각각 1-1B 중 실험 1의 환경에서 발사 실험을 진행해 보았다.
이 구슬들이 발사되었을 때 초기속력을 구하기 위해 2.1.1에서 쓴 두 가지 방법을 모두 쓰기로 했다. 첫 번째 방법은
프레임 사이에서 구한 속력을 쓰는 것이었고, 두 번째 방법은 첫 프레임부터 각 프레임까지 일어난 일에 대한 속력을
쓰는 것이었다. (발사된 각도는 45도다.)

	구슬 R	구슬 G
초기속력(㎨)	1.799	1.449
표준편차	0.096	0.035

표 6: 첫 번째 방법으로 구한 표

	구슬 R	구슬 G
초기속력(㎨)	1.766	1.428
표준편차	0.021	0.013

표 7: 두 번째 방법으로 구한 표

또, 운동 전체를 따져 보았을 때 구슬 R의 초기속력은 1.782(㎨), G는 1.437(㎨)였다.

구슬 G와 R의 궤적을 비교해보면,

그림 6: 구슬 G와 R의 궤적

3. Discussion

실험 데이터에서 오차가 발생한 이유를 설명해보도록 한다.

3.1. 카메라 성능의 한계

실험 데이터에, 분명히 다른 시간에 대한 물체의 물리량임에도 불구하고 같은 물리량으로 카메라가 측정한 부분이 있다.
이는 실험 결과에 큰 오차를 일으킬 수 있는 요인이 되었다.

3.2. 프로그램의 정확도에 대한 한계

I-CA 프로그램이 낙하하는 물체를 인식하는 방식 중 하나가 바로 물체의 색을 보고 인식하는 방식이며, 그것이 우리 조가
사용한 방식이었다. 하지만, 우리가 캡처하고 싶은 물체와는 다른 곳에 있는 부분을 피사체라고 인식하는 등 오차를 일으킬
만한 요인을 일으키는 것을 목격할 수 있었다.

3.3. 낙하 시 초기속도에 대한 영향

물체가 자유낙하를 하도록 하는 실험에서, 물체를 손에서 놓을 때에 물체의 초기 속도가 최대한 0에 가까워지도록,
즉 손의 진동이 거의 없도록 해야 한다. 하지만, 특히 풍선을 매달고 구슬을 떨어뜨리는 실험을 할 때 보면, 낙하 직전에 손의
진동으로 인해 구슬이 많이 흔들리는 모습을 볼 수 있었다. 이 때문에 데이터에 어느 정도 오차가 발생했을 것이라고
추정할 수 있다.

4. Conclusion

실험 1-1A 중 실험 1에서는 자유낙하 운동에 대한 법칙을 확인해보았다. 자유낙하를 하는 물체에 대한 시간-높이 그래프를
그려 보았을 때, 물체가 중력가속도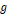 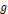로 자유낙하 할 때 그리는 포물선의 그래프와 비슷한 형태의 포물선들이 실험 결과로
그려지는 것을 확인할 수 있었다.

이에 대해 정확히 확인하기 위해서 이 운동에서의 가속도를 측정해보았다. 두 가지 방법으로 측정한 평균적인 가속도는
모두 이론 값인 에 가까웠으나, 특히 첫 번째 방법으로 구한 자료들의 경우에는, 자료들의 표준편차가
상당히 커서 그 평균값에 대한 신뢰도가 떨어지는 것을 확인할 수 있었다. 이는 데이터에 오차가 있었기 때문이었다.
이의 원인으로는 카메라와 프로그램 성능의 한계, 그리고 실험자의 손의 진동 등을 꼽을 수 있었다.

두 번째 방법으로 얻은 결과를 보면 평균적인 가속도의 크기가 중력가속도 보다 작음을 볼 수 있는데, 이는 마찰력의
영향 때문이라고 여겨진다.

실험 1-1A 중 실험 2에서는 부력이 자유낙하 운동에 어떠한 영향을 미치는지 확인할 수 있었다. 마찰력 또한 자유낙하
운동에 영향을 끼칠 수 있으므로, 헬륨이 들어있는 풍선이 매달린 구슬에 대한 낙하 실험을 하는 동시에, 공기가 들어있는
풍선이 매달린 구슬에 대한 낙하 실험을 진행하여 그 둘의 결과를 비교하기로 했다. 두 풍선 모두 공기에 대한 마찰력을
받아 풍선이 없는 구슬에 비해 천천히 떨어지는 것을 관찰할 수 있었으나, 헬륨이 든 풍선에 매달린 구슬의 경우, 공기가 든
풍선에 매달린 구슬에 비해 천천히 떨어지는 것을 발견할 수 있었다. 이를 통해 부력이 중력의 반대방향으로 일부분 작용
하여 자유낙하 운동에 영향을 미쳤음을 확인할 수 있었다.

실험 1-1B 중 실험 1에서는 다양한 각도로 발사한 물체가 어떠한 궤적을 그리면서 날아가는지를 확인하였다. 모두 포물선을
그리면서 날아갔으며, 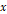축의 관점, 즉 가로에서 볼 때는 등속도 운동과 비슷한 형태의 운동을, 그리고 축의 관점, 즉 세로
에서 볼 때는 등가속도 운동과 비슷한 형태의 운동을 하며 날아갔음을 관찰할 수 있었다. 또, 물체의 발사 지점 높이와 동일
한 높이에 있는 지점까지 물체가 날아간 수평 거리를 따져 보았을 때, 45도로 발사된 물체가 표본 중에서 가장 큰 수평 거리
를 가졌음을 확인할 수 있었다.

실험 1-1B 중 실험 2에서는 다양한 질량을 가진 구슬을 발사해보았다. 발사대에서 구슬을 발사할 때에 항상 동일한 힘을
이용했으나(용수철을 동일한 길이만큼 압축시켰다가 풀었다), 반면 구슬의 질량은 각각 달랐기에 발사된 구슬의 초기 속력
이 각각 다를 수 밖에 없을 것이라고 예상하였다. 예상대로 무거운 구슬의 초기 속력은 가벼운 구슬의 초기 속력보다 작았다.
이러한 이유로 물체가 중력에 의한 운동(포물선 운동)을 할 때에 물체의 질량에 따라 운동 상태가 달라지지는 않는다는 것을
확인하는 것은 불가능했다.

* Reference

1 서울대학교 물리천문학부, 『실험 1-1A. 뉴턴의 사과는 어떻게 떨어졌는가?』, 2015, 5-6