2019년 2월 21일 목요일

[서울대 물리학실험 2-1] 전하와 전하 사이


물리학 실험 2-1

2-1. 전하와 전하 사이

*본 보고서는 이미 제출된 적 있는 보고서로 이를 표절해서 제출하면 무조건 F를 받을 것입니다. 참고용으로만 쓰십시오.

참고: http://physlab.snu.ac.kr/newphyslab/manual/2-1_kr.pdf


I. Introduction

1.1. 실험 목적
대전되어 있는 두 도체 극판 사이에 나타나는 힘을 여러 가지 조건에서 살펴 보고, 쿨롱의 법칙을 간접적으로 확인한다.
1.2. 배경 지식
1.2.1 콘덴서에 저장되는 전하량
콘덴서 판에 저장된 전하량을 , 극판의 면적을 , 극판 사이의 거리를 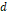, 콘덴서의 전기용량을 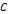, 그리고 진공 중의 유전율을 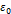라고 하자. 이때, 극판 사이에 유전체가 없는 상태 (진공 상태) 라면 다음과 같이 식을 쓸 수 있다.
또한, 콘덴서의 두 극판 사이의 전위차가 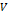라면,
위와 같은 식에 따라 콘덴서 양 극판에 각각 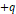, 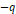의 전하량이 저장된다.
1.2.2 이상적인 콘덴서
본래는 콘덴서의 극판 모서리 부근에서 전기장이 휘어진 모양을 가지므로, 전기장의 모양이 균일하게 되지 않는다. 편의상 이를 무시하고 전기장이 균일한 모양을 보인다고 가정한다.
1.2.3 콘덴서의 에너지 밀도와 전기장
콘덴서의 에너지 밀도를 라고 하면,
이때, 임을 이용하면,
두 판 사이의 균일하게 가정된 전기장 에 대해, 임을 이용하면,
두 극판 중 하나의 극판만을 따졌을 때, 그 한 극판이 만들어내는 전기장의 크기를 라고 한다면,
그러면 두 극판 중 한 극판이 상대 극판의 전기장에 의해 받는 힘의 크기를 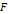라고 한다면,
이때, 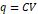임을 이용하면,
1.2.4 콘덴서의 직렬 및 병렬 연결
전기 용량이 각각 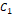, 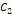인 콘덴서가 연결돼서 전기 용량이 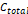인 콘덴서와 동일한 효과를 낸다고 할 때, 콘덴서가 직렬로 연결된 경우,
위 식을 만족하며, 콘덴서가 병렬로 연결된 경우,
1.3. 실험 안내
① 전압 조정 손잡이를 최소로 둔 채, 한 극판은 저울 위에 올리고, 다른 극판은 5mm 정도 간격을 두고 저울 위의 극판과 평행하게 띄운다.
② 극판 사이의 거리를 측정한다.
③ (+) 전극을 위, (-) 전극을 서로 대어 먼저 방전 시킨 뒤, 각각을 위쪽 극판, 아래쪽 극판에 붙인다.
④ 저울 영점을 맞춘 뒤, 전압을 약하게 건다.
⑤ 저울에 표시된 값을 기록하고, 전압을 바꾸어 가며 다시 실험한다.
⑥ 전압 조절 손잡이를 최소로 한 상태에서 극판 사이 거리를 변화시키고, 위와 같이 진행한다.
⑦ 여러 가지 유전체를 극판 사이에 삽입해 가며 위의 과정을 동일하게 진행한다.
⑧ 여러 가지 유전체를 병렬 형태로 극판 사이에 삽입해 가며 위의 실험을 동일하게 진행한다.
2. Data & Result
2.1. 전압의 변화에 따른 결과 (유전체 : 공기)
극판 사이의 간격을 각각 3mm, 4mm, 5mm, 7mm로 한 상태에서 극판 사이의 전위차를 2kV, 4kV, 6kV, 8kV로 변화시키며 저울의 값이 어떻게 변화하는지를 기록하였다. 극판 사이의 유전체는 공기로 둔다. 저울에 표시된 값은 음수이나, 이를 양수로 바꾸어 위쪽 극판이 만드는 전기장에 의해 아래쪽 극판이 받는 힘의 크기를 표시하기로 했다.
그림 1 전압에 따른 실험결과 (전압 오차 : 0.2kV)
극판 사이에서 스파크가 일어났을 때의 실험 데이터는 추가하지 않았으며, 오차 범위를 고려하여 그래프에 오차막대를 추가하였다. (결과 값이 안정적으로 나온 탓에 오차 범위가 작게 설정하여 그림에서는 오차 막대가 잘 보이지 않는다.)
그림 1을 보면 그 그래프가 포물선의 형태를 띠고 있음을 쉽게 짐작할 수 있다.
위의 그래프만으로는 이것이 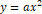의 형태를 잘 띠고 있는지 파악하기 어려우므로, 평균값 정리를 이용하여 위 그래프의 평균 변화율이 그리는 그래프가 일차함수, 즉 직선의 형태를 띠고 있는지 확인하도록 한다.
, 사이의 평균변화율에 대해 아래와 같이 쓸 수 있으므로,
그림 1 그래프의 평균변화율에 대한 그래프는 다음과 같이 그릴 수 있다.
그림 2 평균변화율에 대한 그래프
약 5kV의 전압을 초과하면 평균 변화율의 값이 직선 상에서 벗어나지만, 그 이하의 전압에서는 일정한 직선 상에서 평균 변화율 값이 움직임을 확인할 수 있다.
2.2. 극판 간 간격에 따른 결과 (유전체: 공기)
극판 사이의 전위차를 각각 2kV, 4kV, 6kV, 8kV로 한 상태에서 극판 사이 간격을 3mm, 4mm, 5mm, 7mm로 변화시키며 저울의, 즉 아래쪽 판이 전기장에 의해 받는 힘의 크기가 어떻게 변화하는 지를 기록하였다.
그림 3 간격에 따른 결과 (간격 오차 : 0.5mm)
힘의 크기가 대략 거듭제곱 꼴로 감소하는 형태를 보이기는 하지만, 완벽하게 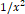로 감소하지는 않고 있다는 것을 확인할 수 있다.
또다른 방법으로, 그림 2의 그래프에 대한 추세선의 기울기를 이용하여 감소 형태를 확인하는 방법이 있다.
극판 사이의 간격을 동일하게 한 상태에서 극판 사이의 전위차를 변화시켰을 때, 위쪽 극판이 만들어내는 전기장에 의해 아래쪽 극판이 받는 힘의 크기를 전위차 에 대해 나타낸 함수 로 다음과 같이 표현하려고 한다.
를 미분하면 인 점을 이용하여, 함수 의 평균 변화율 그래프에 대한 직선 모양 추세선의 기울기를 로 두는 방법을 통해 의 값을 얻어낼 수 있다. (전압 단위는 kV, 힘은 g)
그림 4 간격에 따른 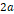의 값
만약, 함수 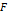가 극판 사이의 간격 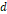의 제곱에 반비례 하다면, 모든 간격에 대해 은 일정해야 할 것이다. 아래는 이에 대한 계산 결과이다. (길이의 단위는 mm로 하였다.)

3mm
1.2743
5.73435
4mm
0.65
5.2
5mm
0.5871
7.33875
7mm
0.2629
6.44105
평균

6.178538
표준편차

0.716916
표 1 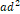의 계산 결과
완전히 안정적으로 일정한 값을 보이지는 않으나, 어느 정도 일정한 값을 유지하는 모습을 보이는 것을 확인할 수 있다. 즉, 함수 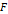가 어느정도 극판 사이의 간격 의 제곱에 반비례 하는 모습을 보인다고 말할 수 있다.
2.3. 유전상수의 비교
2.2에서의 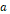의 값을 유전체의 종류 전체로 확장하려고 한다. 공기를 유전체로 뒀을 때 의 값을 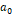, 비교하고자 하는 물질을 유전체로 극판 사이에 삽입했을 때 얻어낸 의 값을 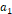이라고 하면, 비교하고자 하는 물질의 유전상수는 이 됨을 이용할 것이다. (단, 공기의 유전율이 진공의 유전율과 거의 같다고 가정한다.)
유전체 판의 두께가 3mm였던 관계로, 극판 사이의 간격을 3mm로 설정하였다. 유리와 아크릴로 제작된 직육면체 형태의 유전체를 극판 사이에 각각 삽입하고, 위쪽 극판이 형성하는 전기장에 의해 아래쪽 극판이 받는 힘의 크기가 전압에 따라 얼마나 달라지는지 측정하였다.
그림 5 전압에 따른 힘의 변화
2.2에서 했던 것과 마찬가지로 평균 변화율에 대한 그래프를 그려 의 값을 구하고자 하였다.
그림 6 평균 변화율에 관한 그래프
그러나 결과는 이론과는 다른 모습을 보여주었다. 유리의 경우 그림 6에서 그래프의 모습이 직선보다는 직선과 포물선 그 중간에 더 가까운 모습을 보이며, 그 기울기가 지나치게 크기 때문이다. 반면, 아크릴의 경우 직선이 아래쪽으로 휘어지는 모습을 볼 수 있다.
안정적이고 정확한 의 값을 구하기 위하여, 평균 변화율에 관한 그래프인 그림 6을 이용하지 않고, 그림 5의 그래프가 의 꼴을 가진다고 가정 한 뒤 이를 이용하기로 한다. 그림 5 그래프의 함수 값을 전위차의 제곱으로 나누는 방법으로 의 값을 구할 수 있을 것이다.
전압
유리
아크릴
1kV
4.6
2.8
2kV
6.15
1.5
3kV
7.888889
1.377778
평균
6.212693
1.892593
표준편차
1.343421
0.643571
표 2 유리와 아크릴의 값
또한, 공기에 대한 의 값을 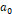이라고 하고, 비교하고자 하는 물질에 대한 의 값을 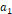,  축전기의 극판 사이 간격을 라고 했을 때, 의 값이 비교하고자 하는 물질의 유전상수의 근사값임을 이용하여 유리와 아크릴의 유전상수를 계산하고자 한다. 이때, 의 값은 표1에서 구한 평균값을 이용할 것이다.

유리
아크릴
평균
9.050146036
2.756855216
표준편차
1.956901743
0.937461376
표 3 유리와 아크릴의 유전상수
유리의 경우 실제 유전상수는 3.7 ~ 10 정도 되며 (또는 5 ~ 10), 아크릴의 경우 실제 유전상수는 2.4~4.5 정도 된다. (2.56이라고 하기도 함) 실험에서 얻어낸 유전 상수 값 모두 이 범위에 포함되므로 실제 값과 어느 정도 유사한 값을 얻어냈다고 말할 수 있겠다.
2.4. 축전기의 병렬 연결
전에 썼던 유전판의 1/2 크기인, 테프론과 아크릴 유전체 판을 가로로 나란하게 극판 사이에 넣었다. 2.2에서 했던 것과 마찬가지의 방법으로 둘이 병렬 연결되었을 때, 축전기가 어떤 유전상수를 가진 효과를 내는지 알아보았다.
그림 7 힘의 변화의 평균 변화율에 관한 그래프
평균 변화율에 대한 그래프가 직선 상에 있다고 간주할 때, 그 기울기는 약 2.1029이므로, 병렬 연결된 유전체에 대한 의 값은 약 1.05145이다. 이 값을 토대로 2.3에서 했던 방법을 이용하여 유전상수를 계산해 보면, 유전상수는 약 2.72284501이 나온다.
2.3에서 도출된 아크릴의 유전상수와 테프론의 유전상수 이론 값 2.1을 이용해서, 병렬 연결된 유전체의 유전상수가 과연 이론에 맞게 나왔는지 확인해 보았다. 만약 이론대로라면, 병렬 연결된 유전체의 유전상수는 다음과 같이 나와야 한다.
값을 비교했을 때 차이가 있긴 하나 어느 정도 유사한 값이 나온 것을 확인할 수 있다.
3. Discussion
데이터에 영향을 주었을 가능성이 있는 요소들로 다음을 꼽을 수 있었다.
3.1. 측정 한계
극판 사이의 간격 등을 정확하게 측정하기에 자의 눈금이 상대적으로 두꺼웠다. 이로 인해 값의 오차가 생겼을 수 있다. 이에 대한 오차막대를 앞서 그래프에 표기하였으나 작아서 보이지가 않을 정도로 이의 영향은 미미할 것으로 보인다.
3.2. 모서리 효과
축전기에 관한 공식들 중 상당수가 모서리 효과가 없다고 가정한 상태에서 내린 공식들이다. 그러나 실험 대상인 축전기에는 모서리 효과가 존재할 수밖에 없기 때문에 데이터에 영향을 주었을 가능성이 높다.
3.3. 축전기 극판의 평행
아래쪽의 극판과 위쪽 극판이 서로 평행해야 하는데, 이것이 완전히 평행하지 않아 데이터에 영향을 주었을 수 있다.
3.4. 유전체 판의 모양
극판이 원형인 것과 달리, 유전체 판의 모양은 사각형이었으며, 이것이 데이터에 어느 정도 큰 영향을 미쳤을 가능성이 있다.
3.5. 완화효과
유전체가 전자기파의 에너지를 흡수하는 과정에서 완화 효과라는 것이 발생하는데, 이것이 데이터에 영향을 주었을 가능성이 있다.
4. Conclusion
우선 극판 사이에 아무것도 끼지 않은 상태 (유전체가 공기인 상태)에서 실험을 진행하여 이론을 간접적으로 확인하고자 하였다. 반대편 극판이 만들어내는 전기장에 의해 한 쪽 극판이 받는 힘이 전위차의 제곱에 비례하고, 극판 사이의 간격의 제곱에 반비례하다는 것이 이론이었다. 실험을 통해 확인해 본 결과, 완벽하지는 않지만 어느 정도 유사하게 전기력이 전위차의 제곱에 비례하고, 극판 간 간격의 제곱에 반비례하다는 것을 확인할 수 있었다.
다음에는 다양한 유전체를 극판 사이에 삽입하면서 실험을 진행하였고, 실험을 통해 얻어낸 유전체의 유전 상수(relative permittivity)와 이론 값을 비교하였다. 확인 결과, 실험 값이 모두 이론적인 유전 상수의 범위 내에 존재한다는 것을 확인할 수 있었다.
마지막으로 두 가지 유전체를 병렬 연결 형식으로 극판 사이에 삽입하여 축전기의 병렬 연결에 관한 이론을 확인해 보았다. 완전 일치는 아니었으나, 어느 정도 이론을 통해 계산한 값과 유사한 값을 실험을 통해 얻어낼 수 있었다.
이론과 완벽하게 일치하지 않았던 이유로 여러 가지를 꼽을 수 있었다. 측정 한계나 모서리 효과, 그리고 유전체 모양이 사각형이라는 사실과 유전체의 충전 과정에서 완화 효과가 일어난다는 사실이 데이터에 영향을 줄 수 있다고 판단하였다.
* Reference
1 서울대학교 물리천문학부, 『실험 2-1, 전하와 전하 사이의 힘』, 2017, 6
3 https://renesasrulz.com/capacitive-touch-cap-touch/f/cap-touch/9775/capacitive-touch-overlay-construction
작성자: 시간:
라벨: , , , , , , ,