물리학실험 2-5
2-5. 휘스톤브리지 실험
*본 보고서는 이미 제출된 적 있는 보고서로 표절 시 발각될 확률이 높으니 참고만 하시길 바랍니다.
1. Introduction
1.1. 실험 목적
휘스톤 브리지의 구조와 원리에 관한 이론을 숙지하고, 휘스톤 브리지를 통해 미지의 전기 저항을 측정하며 이론을 확인한다.
1.2. 배경 지식
1.2.1. 휘스톤 브리지
그림 1 휘스톤 브리지의 구조
다음의 구조를 가지는 회로가 있다.  는 저항 값을 정확히 알고 있는 기지저항이다.
는 저항 값을 정확히 알고 있는 기지저항이다. 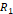 과
과  의 값을 조절하여 BD 사이의 전위차를 0으로 만들었을 때, AD, CD 사이로 흐르는 전류를
의 값을 조절하여 BD 사이의 전위차를 0으로 만들었을 때, AD, CD 사이로 흐르는 전류를 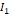 , AB, BC 사이로 흐르는 전류를
, AB, BC 사이로 흐르는 전류를  라고 하면, 다음이 성립한다.
라고 하면, 다음이 성립한다.
이때, 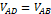 ,
, 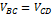 이므로,
이므로,
1.2.2. 습동저항선으로 구성된 브리지
그림 2 Ready-set 휘스톤브리지
Ready-set 휘스톤브리지에서, 직경이 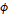 이고 비저항이
이고 비저항이 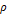 인 균일한 저항선으로 감겨진 솔레노이드형 습동저항선이 직경
인 균일한 저항선으로 감겨진 솔레노이드형 습동저항선이 직경 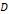 를 가질 때, 저항
를 가질 때, 저항 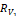 의 길이가
의 길이가 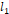 , 저항
, 저항  의 길이가
의 길이가 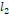 면,
면,
그러므로 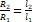 이며, 이를 이용하면,
이며, 이를 이용하면,
1.3. 실험 방법
직류 전원 장치 5V, 기지저항(100Ω, 1kΩ, 10kΩ, 50kΩ, 100kΩ), 미지 저항 12가지, 디지털 검류계1μA, 습동저항선 20cm, 측정용 버니어캘리퍼스, 멀티미터를 준비한다.
① Ready-set 휘스톤브리지 실험 기구를 준비하고, 전원을 연결한다. (전압은 5V로 고정됨)
②  다이얼을 돌려 미지저항 1번을 선택하고, 검류계 스위치를 ON으로 돌린다.
다이얼을 돌려 미지저항 1번을 선택하고, 검류계 스위치를 ON으로 돌린다.
③ 습동저항선 단자를 가운데 근처에 두고, 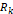 의 다이얼을 돌려 경보음이 들리지 않도록
의 다이얼을 돌려 경보음이 들리지 않도록  을 설정한다. 이러한
을 설정한다. 이러한 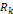 가 없으면 최대한 가운데에 가까운 쪽으로
가 없으면 최대한 가운데에 가까운 쪽으로 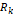 를 선정한다.
를 선정한다.
④ 습동저항선 단자의 위치를 조정해서 검류계에 표시되는 값이 0이 되도록 하고, 이때 단자의 위치를 부착된 버니어캘리퍼스로 읽는다.
⑤ 미지 저항의 값을 계산한 후 기록한다.
⑥  를 2~12번까지 변화시키며 위의 과정을 반복한다.
를 2~12번까지 변화시키며 위의 과정을 반복한다.
⑦ 멀티미터로 미지 저항을 직접 측정하거나 저항의 띠로 미지 저항의 실제 값을 얻고, 이를 실험을 통해 얻은 값과 비교한다.
2. Data & Result
미지저항을 바꿔가면서 배경 지식 중 1.2의 식을 그대로 이용해서 계산했을 때 산출된 미지저항의 값과 실제 미지저항의 값이 얼마나 다른 지 표를 통해 확인해 보았다.
번호
|
실제값
(Ω)
|
허용
오차율(
|
실험값
(Ω)
|
실제와 오차(%)
|
1
|
1500
|
10
|
1490.66
|
-0.6227
|
2
|
470
|
5
|
467.3514
|
-0.5635
|
3
|
3000
|
5
|
2987.22
|
-0.426
|
4
|
8200
|
10
|
8382.353
|
2.22382
|
5
|
2700
|
5
|
2674.597
|
-0.9408
|
6
|
12000
|
10
|
12467.53
|
3.8961
|
7
|
560
|
10
|
571.0919
|
1.9807
|
8
|
820
|
10
|
809.9548
|
-1.225
|
9
|
4700
|
5
|
4737.098
|
0.78933
|
10
|
18000
|
5
|
19177.28
|
6.54043
|
11
|
5600
|
5
|
5660.981
|
1.08894
|
12
|
2200
|
5
|
2183.908
|
-0.7315
|
표 1 미지저항에 대한 실제 값과 실험값의 비교
다음과 같이 10번 미지저항을 제외한 나머지 실험값은 실제 값과의 차이가 허용 오차율 이내에 있었다. 1~3번과 5번, 9번, 12번은 오차율이 0% 이내에 있는 등 상당히 정확도가 높은 모습을 보여주었다. 10번 미지저항의 경우에도 허용 오차율을 벗어나긴 했으나 그 값이 실제 값과 매우 유사하였다. 전체적으로, 1.2.2의 식으로 계산한 실험 값과 실제 값이 매우 유사하며 그 정확도가 높았다고 결론을 내릴 수 있었다.
3. Discussion
실험을 얻은 데이터에 이론을 적용해서 얻은 미지 저항의 값과 실제 미지 저항의 값의 유사도가 매우 높았으나, 10번처럼 어느 정도 오차율이 있던 경우도 있었다. 여기서는 그러한 오차의 원인에 대해서 분석해 보도록 한다.
3.1. 습동저항선의 비균등성
1.2.2에서는 습동저항선을 이루는 도선의 비저항과 단면의 크기가 일정하고, 습동저항선의 직경 또한 일정하다고 가정하였으나, 실제로는 그렇지 않을 가능성이 매우 높다. 이로 인해 실험 값과 실제 값 사이에 차이가 발생했을 수 있다.
이러한 오차의 영향이 얼마나 큰지 검증하기 위해서 1번 데이터를 측정할 때 멀티 미터를 이용하여 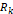 에 걸린 전압과
에 걸린 전압과 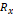 에 걸린 전압의 비를 얻어냈다. 그 전압의 비는 2:3이었으며, 오차는 멀티미터에 그려진 눈금의 두께 정도일만큼 그 비의 값은 매우 정확했다. 1번 데이터를 측정할 때
에 걸린 전압의 비를 얻어냈다. 그 전압의 비는 2:3이었으며, 오차는 멀티미터에 그려진 눈금의 두께 정도일만큼 그 비의 값은 매우 정확했다. 1번 데이터를 측정할 때  의 값은 1000 Ω이었으므로, 이 비를 통해 계산한
의 값은 1000 Ω이었으므로, 이 비를 통해 계산한 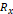 의 값은 1500Ω이며, 표 1에서 이 값은 실험 데이터를 1.2.2에서의 공식에 대입했을 때 얻어낸 값인 1490.66Ω과 약 0.63%의 오차밖에 보이지 않았던 값이다. 이러한 정확도는 습동 저항선이 어느 정도 균등할 때 얻어낼 수 있는 정확도이므로, 습동저항선의 비균등성은 오차의 큰 원인은 되지 못한다고 결론을 내릴 수 있었다.
의 값은 1500Ω이며, 표 1에서 이 값은 실험 데이터를 1.2.2에서의 공식에 대입했을 때 얻어낸 값인 1490.66Ω과 약 0.63%의 오차밖에 보이지 않았던 값이다. 이러한 정확도는 습동 저항선이 어느 정도 균등할 때 얻어낼 수 있는 정확도이므로, 습동저항선의 비균등성은 오차의 큰 원인은 되지 못한다고 결론을 내릴 수 있었다.
3.2. 저항의 불량
저항이 띠에 명시되어 있는 것만큼 정확하게 저항 값을 가지지 못하고 오차를 보였을 확률이 매우 크다. 불량인 저항이 기기에 사용되었을 가능성이 매우 작게 나마 있긴 하나, 미지 저항이 허용 오차율 내의 저항 값을 가지고 있다고 해도 이러한 오차가 위에서의 습동 저항선의 비균등성과 같은 다른 오차 원인과 함께 시너지를 일으켜 오차를 크게 만들었을 가능성이 있다고 보았다.
3.3. 인간의 기기 조작 한계
본래 정확한 실험 데이터를 얻어내기 위해선 회로에 연결된 검류계가 정확히 0이라는 값을 띄울 때 실험 데이터를 얻어내야 하지만, 인간의 기기 조작엔 한계가 있는 탓에 검류계가 정확히 0이라는 값을 띄우지 못했을 때 실험 데이터를 얻어낸 경우가 몇 번 있었다. 이러한 이유 때문에 오차를 일으켰을 가능성이 있다.
3.4. 기기의 성능 한계
인간과 마찬가지로 기기도 정확하게 성능을 내지 못할 때가 있는데, 이러한 이유로 데이터에 오차를 일으켰을 가능성이 있다고 보았다.
3.5. 오차 원인을 고려한 결과값
위에서 언급한 오차를 고려했을 때, 미지 저항의 저항 값을 1.2.2의 공식을 통해 계산한 결과 값은 아래와 같다.
번호
|
오차 고려 최대값(Ω)
|
오차 고려 최솟값(Ω)
|
실제와
최대와
차이(%)
|
실제와
최소와
차이(%)
|
1
|
1522.068096
|
1460.0246
|
1.4712
|
-2.665
|
2
|
478.1966001
|
456.6642389
|
1.744
|
-2.837
|
3
|
3051.529791
|
2923.930269
|
1.7177
|
-2.536
|
4
|
8552.875696
|
8214.936248
|
4.3034
|
0.1821
|
5
|
2733.952049
|
2616.14623
|
1.2575
|
-3.106
|
6
|
12733.22422
|
12206.11916
|
6.1102
|
1.7177
|
7
|
583.5312747
|
558.8464536
|
4.202
|
-0.206
|
8
|
826.4840183
|
793.7219731
|
0.7907
|
-3.205
|
9
|
4832.841691
|
4643.201543
|
2.8264
|
-1.208
|
10
|
19564.78734
|
18797.28419
|
8.6933
|
4.4294
|
11
|
5775.862069
|
5548.523207
|
3.1404
|
-0.919
|
12
|
2235.890014
|
2132.667618
|
1.6314
|
-3.061
|
표 2 오차의 값
오차를 적용해도 실제 값과의 차이가 크게 나지는 않음을 알 수 있다. 허용 오차율을 넘어선 것도 10번밖에 없었으며, 10번 또한 오차값 중 최솟값인 경우에는 그 값이 허용 오차율 이내에 들기도 했다.
4. Conclusion
이 실험에서는 휘스톤 브리지를 이용해서 미지 저항의 저항 값을 측정하는 실험을 진행하였다. 이 실험에서는 Ready-set 휘스톤 브리지를 사용하였는데, 습동저항선 도선의 비저항과 단면적, 그리고 습동저항선의 단면적(직경) 또한 일정하다고 가정하여 얻어낸 간소화된 공식(1.2.2 참고)을 미지 저항의 저항 값을 산출하는데 이용하였다.
실험 데이터를 얻어내고 미지 저항의 저항 값을 산출한 결과, 거의 대부분의 경우 실험 값과 실제 값과의 오차율이 허용 오차율 이내에 들 정도로 매우 높은 정확도를 보여주었다.
하지만 이 실험 데이터에서도 오차가 존재하긴 했으므로, 그 오차의 존재 원인에 대해서 여러 가지를 꼽았다. 그 원인으로 습동저항선의 비균등성, 저항의 불량, 인간의 기기 조작 한계, 기기의 성능 한계를 꼽을 수 있었다.
이러한 오차 원인을 고려하여 결과 값을 산출하였는데, 그 값을 분석한 결과 오차가 실험 값과 실제 값 사이의 정확도를 의미 있게 낮출 정도로 크지 않다고 판단하였다. 그러한 이유로, 실험 값과 실제 값 사이의 정확도가 매우 높다는 결론을 뒤집지 않았다.
*Reference
1 <2-5. 휘스톤브리지 실험>, 《Physics Laboratory》, 서울대학교 물리천문학부 편, 2017, 4-6면.
*실험 데이터
아래는 미지 저항에 대한 결과 값의 자세한 데이터이다.
번호
|
허용
오차율(%)
|
실험값
(Ω)
|
실제와의 오차율(%)
| ||||
1
|
8.03
|
11.97
|
1000
|
1500
|
10
|
1490.66
|
-0.62267
|
2
|
13.63
|
6.37
|
1000
|
470
|
5
|
467.3514
|
-0.56353
|
3
|
12.52
|
7.48
|
5000
|
3000
|
5
|
2987.22
|
-0.42599
|
4
|
10.88
|
9.12
|
10000
|
8200
|
10
|
8382.353
|
2.223816
|
5
|
13.03
|
6.97
|
5000
|
2700
|
5
|
2674.597
|
-0.94085
|
6
|
12.32
|
7.68
|
20000
|
12000
|
10
|
12467.53
|
3.896104
|
7
|
12.73
|
7.27
|
1000
|
560
|
10
|
571.0919
|
1.980698
|
8
|
11.05
|
8.95
|
1000
|
820
|
10
|
809.9548
|
-1.22503
|
9
|
10.27
|
9.73
|
5000
|
4700
|
5
|
4737.098
|
0.789326
|
10
|
10.21
|
9.79
|
20000
|
18000
|
5
|
19177.28
|
6.540429
|
11
|
9.38
|
10.62
|
5000
|
5600
|
5
|
5660.981
|
1.088943
|
12
|
13.92
|
6.08
|
5000
|
2200
|
5
|
2183.908
|
-0.73145
|