[서울대 물리학실험 1-7] 용수철 흔들이의 운동

물리학 실험 1-7

1-7. 용수철 흔들이의 운동

*본 보고서는 이미 제출된 보고서로 표절 시 발각될 확률이 높으니 참고만 하시길 바랍니다.

1. Introduction

1.1. 실험 목적

① 용수철에 추를 매달아 수직 진동자로 사용하고, 길이가 고정된 실에 추를 매달아 흔들이를 만들어 단조화 운동에 대해서 알아보도록 한다.

② 추가 매달린 용수철을 흔들이로 사용할 때의 물체의 운동을 조사한다.

③ 단조화 운동과 비선형 효과에 대해서 공부한다.

1.2. 배경 지식

1.2.1 미분 방정식

중력 하에서 용수철에 매달린 물체의 상하 운동에 대하여, 중력 가속도를 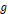, 용수철 상수를 , 물체의 질량을 , 늘어난 길이를 라 하면, 물체에 가해진 알짜힘은 다음과 같다.

이 미분 방정식의 해는 다음과 같다.

여기서 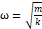, 이며, 진폭 와 위상 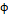는 초기 조건에 의해 결정된다.

1.2.2 질량이 있는 용수철에서의 단진동

질량이M인 균일한 용수철을 생각하면, 용수철의 늘어난 길이는 위치에 따라 달라져 다음과 같다.

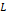이때, 는 중력이 없었을 때의 용수철 상수, 은 용수철의 길이, 는 용수철을 매단 곳으로부터의 거리이다.x

또, 용수철 상수에 대해,

이 용수철의 평균 용수철 상수는

일 경우, 위의 식은 다음으로 근사한다.

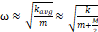이때, , 로 근사한다.

1.2.3 흔들이

길이 L이 일정한 흔들이의 경우 수직 방향으로부터 각도 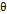만큼 기울어진 질량 M의 복원력에 대하여

일 때 운동 법칙은

이를 풀면 다음과 같다.

여기서 각속도 , 주기 이다.

또, 초기 조건을 이용하면

1.2.4 일반적인 물체의 흔들이 운동

매달린 물체의 관성 모멘트를 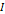라고 하고, 고정된 점으로부터 물체의 질량 중심까지의 거리를 라고 하면, 흔들이 운동의 주기는 다음과 같다.

1.2.5 단순조화운동에서의 에너지

단순 조화 운동에서 총 역학적 에너지는 보존된다.

1.2.6 리사쥬 도형

수직으로 일어나는 두 단조화 운동을 합성하면 리사쥬 도형을 볼 수 있다.

이때, 두 운동의 진동수와 위상이 같다면,

1.2.7 공기의 쓸림힘

속도에 비례하게 공기의 쓸림힘을 받는다고 하면,

1.3. 실험 안내

용수철, 용수철용 스탠드, 컴퓨터, CCD 카메라, 실, 추 등등을 준비한다.

1.3.1 용수철의 단진동

① 추의 무게에 따른 용수철의 길이 변화를 측정하여 용수철 상수를 구한다.

② 추의 운동을 상하 운동에 국한시키고, CCD 카메라 및 컴퓨터로 추의 단조화 운동을 캡처한다.

③ 저울로 추와 용수철의 무게를 측정한다.

④ 자료를 이용해 이론값과 비교한다.

1.3.2 흔들이 운동

① 적당한 길이의 실로 흔들이를 만들고, 이의 운동을 캡처한다.

② 실의 길이를 바꾸어 다시 실험한다.

③ 자료를 분석한다.

1.3.3 리사쥬 도형

용수철에 매달린 추를 아래로 당긴다. 당긴 상태에서, 수평 위치에서 일정 각도로 이동시켜 운동을 시킨다. 이 운동을 캡처한다. 자료를 분석하고 리사쥬 도형을 그린다.

2. Data & Result

2.1. 용수철 상수의 측정

여러 질량의 추를 용수철에 달아서 용수철 상수를 측정해보려고 한다. 이 용수철이 균일한 용수철인지 검증할 수 있을 것이다. 이 측정에서 사용된 용수철의 질량은 14g이었고, 추 받침대의 질량은 66g이었다. . 다만, 오차를 줄이기 위해서 상수 측정 시 어떤 질량의 추가 매달린 용수철의 길이에서 10g의 추가 매달린 용수철의 길이를 뺀 값을 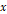(cm)로 두고 측정하기로 했다. 10g의 추를 매달았을 때 용수철의 길이는 26cm였다. (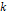는 중력이 없을 때의 용수철 상수)

추 질량(g)	용수철 길이(cm)
49.5	35.8	3.9527	4.1191
20	29	3.2689	3.4564

표 1 용수철 상수의 측정

이때 의 평균값은 3.8597(N/m)였다.

2.2. 용수철의 단진동 실험

용수철에 추를 매달고 단진동을 일으키는 실험을 하였다. 용수철에 추 받침대를 매달고 추 받침대 안에 추를 넣고 단진동을 일으키는 형식으로 실험을 진행하였기에, 가벼운 추를 넣으면 추가 진동 도중에 붕 뜨는 일이 발생하기도 하였다. 그래서 무게가 비교적 무거운 추에 대한 실험 결과를 중심적으로 분석하기로 했다.

다음은 49.5g짜리 추를 매달고 한 실험이다. 추 받침대의 무게는 66g이었다.

그림 1 49.5g 추의 단진동 1

그림 2 49.5g 추의 단진동 2

이 데이터에서 주기를 구했다. 실험을 통해 얻은 주기와 이론을 통해 얻은 주기의 값을 비교하기로 하였는데, 이때 1.2.2에서 얻은 식 대신 그보다 더 정확한 이 식을 사용하기로 했다.

다음은 그 결과이다. (시간 단위는 초이다.)

	실험값	이론값
1	1.1334	1.1089
2	1.125	1.1089

표 2 49.5g 추의 주기

그리고 이번엔 10g 질량을 가진 추로 실험을 진행하였다.

그림 3 10g 추의 단진동

그리고 실험을 통해 얻은 주기는 약 0.9257초였고, 이론을 통해 얻은 주기는 약 0.9085초였다.

2.3. 흔들이 실험

이번에는 실에 추를 매달고 흔들이 실험을 진행하였다. 실의 길이는 약 36.8cm였다.

그림 4 실 36.8cm의 흔들이 1

그림 5 실 36.8cm의 흔들이 2

그리고 이것은 주기에 대한 결과이다. 우선 수평면에 대하여 주기를 계산하였다.

	실험값	이론값
1	1.266	1.2171
2	1.233	1.2171

표 3  실 36.8cm의 수평면 주기

그 다음엔 수직면에 대하여 주기를 계산하였다. 비교적 그 운동의 형태가 뚜렷하게 드러나는 첫 번째 실험 결과를 가지고 계산하였다. 실험을 통해 구한 주기는 약 0.666초였고, 이론을 통해 구한 주기는 약 0.6086초였다.

다음에는 실의 길이를 약 32cm로 잡고 실험을 진행하였다. 문제는 추가 지속적으로 회전하여 카메라가 인식을 매우 힘들어한다는 것이었다. 비교적 형태가 뚜렷하게 보이는 부분을 발췌하여 수평면에 대한 주기를 구해냈다. 실험을 통해 구한 주기는 약 1초였고, 이론을 통해 구한 주기는 약 1.135초였다.

2.4. 두 단조화운동의 합성

49.5g짜리 추를 용수철에 단 뒤, 용수철을 늘린 상태에서 용수철을 기울인다. 기울인 용수철을 놓으면 두 단조화 운동이 합성되는 효과가 나타나는데, 그 운동을 수평면과 수직면 운동으로 나누어 그림을 그려보았다.

그림 6 합성 운동의 궤적 1

그림 7 합성 운동의 궤적 2

이를 도형으로 나타냈을 때 리사쥬 도형의 형태를 가지게 되었다.

3. Discussion

이 실험 결과에 영향을 줄 수 있었던 요인들은 다음과 같다.

3.1. 옆 돌기

흔들이에서 떨기의 각도가 너무 크면 옆 돌기(세차 운동)이 일어나 실험 결과에 영향을 주게 된다.

3.2. 카메라 및 프로그램의 성능 한계

프로그램이 작은 길이의 변화는 제대로 측정하지 못하고 물체가 같은 위치에 있다고 판단하는 경우가 매우 잦았다. 이것이 실험 결과에 영향을 줄 수 있다.

3.3. 추의 들썩임

진동의 진폭이 너무 크면 추 받침대에 놓인 추가 들썩이는 일이 발생할 수 있다. 이것이 실험 결과에 영향을 미칠 수 있다.

3.4. 공기의 쓸림힘

공기의 저항 및 공기의 쓸림힘이 실험 결과에 영향을 줄 수 있다고 판단하였다. 그 영향이 실제로 얼마나 미쳤는지 확인하기 위해 최고와 최저 진폭의 평균값이 시간에 따라 어떻게 변하는지 확인해보았다. 아래는 2.1에서의 첫 번째 실험 데이터를 토대로 내놓은 결과이다.

그림 8 2.1 첫 번째 실험 진폭의 평균값 변화

위와 같이 그 변화가 거의 없는 것을 확인할 수 있는데, 이로써 공기의 쓸림힘으로 인한 영향이 거의 없다고 가정할 수 있음을 보일 수 있다.

3.5. 균일하지 않은 용수철

실험 도중 용수철이 늘어나는 모습을 지켜 보았을 때, 용수철의 어느 부분은 잘 늘어나는 반면 어느 부분은 잘 늘어나지 않는 등 용수철이 균일하게 늘어나지 않는 등 처음에 내린 가정과는 다른 용수철의 모습을 볼 수 있었다. 이것이 실험 결과에 영향을 미쳤을 수 있다.

4. Conclusion

이 실험을 진행한 결과, 여러가지 이론들을 시험해 볼 수 있었다. 첫 번째는 용수철의 단조화 운동이었다. 49.5g의 질량을 가진 추와 10g의 질량을 가진 추를 이용하여 실험을 진행하였다. 우선 시간에 따른 추의 위치가 이론에 맞게 코사인 함수의 형태를 가지고 있었다. 위치의 주기 또한 이론으로 추론해낸 값과 어느 정도 유사한 값을 가지고 있었다.

두 번째는 흔들이 운동이었다. 길이 36.8cm의 실과 길이 32cm의 실을 이용하여 실험을 진행하였다. 우선 수평면에 대한 운동의 주기와 수직면에 대한 운동의 주기를 비교한 결과, 수직면에 대한 주기는 수평면에 대한 주기의 약 0.5배였다. 추가 한쪽 끝에서 다른 쪽 끝으로 갈 때 수직면에 대해서는 한 번 진동한 것이지만, 수평면에 대해서는 반 번 진동한 것이라는 직관적 사고에 맞는 결과를 보여준다. 또한, 추의 위치가 그리는 함수 또한 이론에 부합하게 코사인 함수의 형태를 가지고 있었다. 위치의 주기도 이론으로 추론해낸 값과 어느 정도 유사한 값을 가지고 있었다.

세 번째는 두 단조화 운동의 합성이었다. 49.5g의 추를 용수철에 매달아 실험을 두 번 진행하였는데, 두 번 모두 결과로 나온 그래프는 리사쥬 도형의 형태를 가지고 있었으며, 이 결과는 이론에 어느 정도 부합하는 결과이다.

실험 결과가 이론 값과 어느 정도 유사성을 보이나, 그래도 차이가 있음을 분명하게 말할 수 있었다. 그 이유로 추의 옆 돌기나 들썩임, 균일하지 않은 용수철, 그리고 카메라와 프로그램의 성능적인 한계를 들 수 있었다.

위와 같은 요인들이 있었음에도 불구하고, 실험 결과와 이론 값이 큰 유사성을 보이는 것으로 보아, 전체적으로 실험 결과가 이론에 부합하다고 말할 수 있을 정도로 나왔다고 말할 수 있었다.

*Result

1 J. M. Nunes da Silva, Am. J. Phys. 62, 423 (1994)