Programming Assignment #5
*본 보고서는 이미 제출된 보고서로 표절 시 발각될 확률이 높으니 참고만 해주시길 바랍니다.
<제목 차례>
I. Introduction
1. Program
2. Condtions
2. Programming
1. Background
2. Input & Output
3. Procedure
3. Result
<수식 차례>
수식 1 단순한 선형 사상
수식 2 평행 이동까지 포함한 식
수식 3 평면 상의 평행 이동을 표현한 식
수식 4 삼각형에 대한 이동
수식 5 행렬식을 구하는 식
수식 6 역행렬을 구하는 식
수식 7 회전의 선형 사상
수식 8 확대의 선형 사상
수식 9 평행 이동의 선형 사상
<그림 차례>
그림 1 행렬식을 구하는 과정
그림 2 역행렬을 구하는 과정
그림 3 ~ 11 Input & Output
그림 12 ~ 17 코드
그림 18 ~ 19 변환 사상 결과
그림 20 ~ 23 PostScript 출력 결과
I. Introduction
1. Problem
① 주어진 삼각형에 대해 다음의 작업을 수행하고 각 과정마다 변하는 삼각형의 모습을 PostScript를 통해 확인하여라.
A. 원점을 중심으로 10도 회전
B.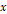 
축 방향으로 2배, 
축 방향으로 3배 확대
축 방향으로 2배, 축 방향으로 3배 확대
C. 
축 방향으로 +50, 
축 방향으로 -50 이동
축 방향으로 +50, 축 방향으로 -50 이동
② 원래 Domain의 삼각형과 PostScript Domain의 삼각형이 주어져 있을 때 변환할 수 있는 선형 사상을 구하여라.
③ ②번 과정을 직접 손으로 풀어보고 결과가 같음을 보이라.
2. Conditions
C#으로 프로그래밍이 이루어져야 한다. 그리고 주어진 삼각형을 구성하는 점들의 좌표는 다음과 같다.
①번 문제에서 Domian의 삼각형 : (100, 100), (200, 100), (100, 200)
②번 문제에서 PostScript Domain의 삼각형 : (150, 150), (300, 200), (50, 300)
II. Programming
1. Background
2차원의 직교 좌표계에 점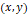 
가 있다고 하자. 이를 선형 사상을 이용하여 점을 ‘이동’시키고자 할 때에는 행렬을 이용하게 되는데, 그 선형 사상을 행렬 
로 표현할 수 있다고 하고, 그 이동 결과가 바로 점 
라면, 다음과 같은 식으로 표현할 수 있게 된다.
가 있다고 하자. 이를 선형 사상을 이용하여 점을 ‘이동’시키고자 할 때에는 행렬을 이용하게 되는데, 그 선형 사상을 행렬 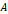로 표현할 수 있다고 하고, 그 이동 결과가 바로 점 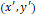라면, 다음과 같은 식으로 표현할 수 있게 된다. 
수식 1 단순한 선형 사상
하지만 선형 사상을 넘어서 평행 이동까지 점의 이동 과정에 포함시키기 위해서는 2차원의 범위 내에서는 다음과 같이 표현할 수밖에 없다. (평행 이동을 위해 사용하는 벡터가 
이다.)
이다.)
수식 2 평행 이동까지 포함한 식
3차원으로 눈을 넓히면, 평면 상의 평행 이동을 식으로 표현할 수 있다. 
라고 한다면, 행렬 
를 아래와 같이 써서 식을 만들 수 있다.
라고 한다면, 행렬 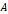를 아래와 같이 써서 식을 만들 수 있다.
수식 3 평면 상의 평행 이동을 표현한 식
만약 점 3에 관해서 이동을 하고 싶다면 다음과 같이 쓸 수 있을 것이다.
수식 4 삼각형에 대한 이동
여기에 대한 행렬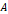 
를 구하기 위해서는 원래의 삼각형 좌표에 대한 행렬의 역행렬을 구해서 변환된 삼각형 좌표에 대한 행렬에 곱해야 한다.
를 구하기 위해서는 원래의 삼각형 좌표에 대한 행렬의 역행렬을 구해서 변환된 삼각형 좌표에 대한 행렬에 곱해야 한다.
역행렬을 구하기 위해서는 행렬식을 알고 있어야 한다. 우선, 2x2짜리 정사각행렬 
에 대해서 행렬식은 
이다. 그리고 nxn짜리 정사각행렬에 대해서 행렬식을 구하는 방법은 다음과 같다.
에 대해서 행렬식은 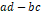이다. 그리고 nxn짜리 정사각행렬에 대해서 행렬식을 구하는 방법은 다음과 같다. 
그림 1 행렬식을 구하는 과정
어떤 정사각행렬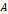 
의 요소 중 첫 번째 행에 있는 요소 
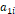에 대해 생각해보자. 그 요소 
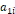가 포함되어 있는 행과 열에 위치한 요소들을 모두 제외한 부분, 즉 그림 1에서의 파란색 부분의 요소를 모두 가져와서 그 요소의 순서가 뒤바뀌지 않도록 부분들을 붙여서 새로운 행렬을 만든다. 그 행렬의 행렬식을 
라고 할 때, 전체 행렬의 행렬식은 다음과 같이 쓸 수 있다.
의 요소 중 첫 번째 행에 있는 요소 에 대해 생각해보자. 그 요소 가 포함되어 있는 행과 열에 위치한 요소들을 모두 제외한 부분, 즉 그림 1에서의 파란색 부분의 요소를 모두 가져와서 그 요소의 순서가 뒤바뀌지 않도록 부분들을 붙여서 새로운 행렬을 만든다. 그 행렬의 행렬식을 라고 할 때, 전체 행렬의 행렬식은 다음과 같이 쓸 수 있다.
수식 5 행렬식을 구하는 식
행렬식을 이용하여 nxn짜리 정사각행렬에 대한 역행렬을 구하는 과정은 다음과 같다.
그림 2 역행렬을 구하는 과정
행렬식의 값이 0이 아닌 정사각행렬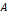 
의 어떤 요소 
에 대하여 생각해 보자. 그 요소가 포함되어 있는 행과 열에 위치한 요소들을 모두 제외한 부분, 즉 그림 2에서의 파란색 부분의 요소를 모두 가져와서 그 요소의 순서가 뒤바뀌지 않도록 부분들을 붙여 새로운 행렬을 만든다. 그 행렬의 행렬식을 
라고 한다면, 역행렬 
는 다음과 같이 쓸 수 있다.
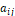의 어떤 요소 에 대하여 생각해 보자. 그 요소가 포함되어 있는 행과 열에 위치한 요소들을 모두 제외한 부분, 즉 그림 2에서의 파란색 부분의 요소를 모두 가져와서 그 요소의 순서가 뒤바뀌지 않도록 부분들을 붙여 새로운 행렬을 만든다. 그 행렬의 행렬식을 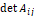라고 한다면, 역행렬 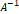는 다음과 같이 쓸 수 있다.
수식 6 역행렬을 구하는 식
반대로, 주어진 변환을 수행하는 선형 사상을 구하는 방법에 대해 다음과 같이 말할 수 있다. 첫 번째로, 어떤 직교 좌표계에서 점을 평면 
상에서 
만큼 회전하는 식은 다음과 같다.
상에서 만큼 회전하는 식은 다음과 같다.
수식 7 회전의 선형 사상
두 번째로, 직교 좌표계 전체를 
축 방향으로 
만큼, 
축 방향으로 
만큼 늘였을 때, 점의 이동을 설명하는 식은 다음과 같다.
축 방향으로 만큼, 축 방향으로 만큼 늘였을 때, 점의 이동을 설명하는 식은 다음과 같다.
수식 8 확대의 선형 사상
세 번째로, 점을 평면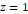 
위에서 
축 방향으로 
, 
축 방향으로 
만큼 평행 이동시키는 사상에 대해서 다음과 같이 쓸 수 있다.
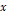위에서 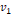축 방향으로 , 축 방향으로 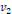만큼 평행 이동시키는 사상에 대해서 다음과 같이 쓸 수 있다.
수식 9 평행 이동의 선형 사상
2. Input & Output
다음은 프로그램 전체와 함수 개별에 대한 실질적인 Input과 Output이다.
그림 3 프로그램 전체, 또는 Main 함수에 대한 실질적인 Input과 Output
원래 Domain의 삼각형의 좌표 정보와 PostScript Domain에서의 삼각형 좌표 정보가 Input으로 주어지며, 이를 받고 변환 전의 삼각형 모습을 output1.ps로, 회전 후의 삼각형 모습을 output2.ps로, 확대 후의 삼각형 모습을 output3.ps로, 평행 이동 후의 삼각형 모습을 output4.ps로 내보내고, Domain 삼각형을 PostScript Domain 삼각형으로 변환시키는 행렬을 Output으로 내보낸다.
Triangle 클래스 내부의 Draw 함수의 실질적인 Input과 Output은 다음과 같다.
그림 4 Triangle 클래스 내의 Draw 함수
파일명(또는 파일 경로)을 Input으로 받고, Triangle 내에 주어진 삼각형의 좌표를 이용해서 삼각형을 그리는 PostScript 파일을 Output으로 내보낸다.
Transformation 클래스 내부의 함수 Multiply에 대한 실질적인 Input과 Output은 다음과 같다.
그림 5 Transformation 클래스 내의 Multiply에 대한 Input과 Output
두 개의 행렬을 Input으로 받은 뒤, 그 둘을 순서에 따라 곱한 결과를 result로 내보낸다.
그림 6 Transformation 클래스 내의 Rotate에 대한 Input과 Output
Rotate 함수의 경우 ref가 붙은 행렬과, 각도의 값을 Input으로 받고, 각도에 맞게 회전시킨 삼각형을 Input으로 받은 행렬에 저장하여 Output으로 내보낸다.
그림 7 Transformation 클래스 내의 Magnify에 대한 Input과 Output
Magnify 함수의 경우 ref가 붙은 행렬과 x와 y라는 두 실수를 받고, 행렬에 저장된 삼각형을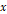 
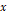축 방향으로 x만큼, 
축 방향으로 y만큼 확대시키고 이를 다시 행렬에 저장하여 Output으로 내보낸다.
축 방향으로 x만큼, 축 방향으로 y만큼 확대시키고 이를 다시 행렬에 저장하여 Output으로 내보낸다.
그림 8 Transformation 클래스 내의 Translation에 대한 Input과 Output
Translation 함수의 경우 ref가 붙은 행렬과 x와 y라는 두 실수를 받고, 행렬에 저장된 삼각형을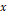 
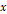축 방향으로 x만큼, 
축 방향으로 y만큼 평행이동을 시킨 뒤 이를 다시 Input으로 받았던 행렬에 저장하여 Output으로 내보낸다.
축 방향으로 x만큼, 축 방향으로 y만큼 평행이동을 시킨 뒤 이를 다시 Input으로 받았던 행렬에 저장하여 Output으로 내보낸다.
그림 9 Transformation 클래스 내의 Transpose에 대한 Input과 Output
Transpose 함수의 경우 ref가 붙은 행렬을 받고, 이의 전치행렬을 Input으로 받았던 행렬에 다시 저장하여 Output으로 내보낸다.
그림 10 Transformation 클래스 내의 Det에 대한 Input과 Output
Det 함수의 경우 행렬을 Input으로 받고, 이의 행렬식 값을 리턴 값으로 내보낸다.
그림 11 Transformation 클래스 내의 GetMap에 대한 Input과 Output
GetMap 함수의 경우 x와 y라는 행렬 두 개를 Input으로 받고, x를 y로 변환시키는 사상 result를 리턴 값으로 내보낸다.
3. Procedure
Class Transformation에 대해서는 다음과 같은 코드를 사용하였다.
namespace triangle
{
class Transformation
{
public static double[,] Multiply(double[,] mat1, double[,] mat2)
{
double[,] result = new double[mat1.GetUpperBound(0)
+ 1, mat2.GetUpperBound(1) + 1];
if (mat1.GetUpperBound(1) ==
mat2.GetUpperBound(0))
{
for (int i = 0; i <=
mat1.GetUpperBound(0); i++)
{
for (int j = 0; j <=
mat2.GetUpperBound(1); j++)
{
double sum = mat1[i, 0] *
mat2[0, j];
for (int k = 1; k <=
mat1.GetUpperBound(1); k++)
{
sum += mat1[i, k] *
mat2[k, j];
}
result[i, j] = sum;
}
}
return result;
}
else
{
Console.WriteLine("Cannot
Multiply those!");
return result;
}
}
public static void Rotate(ref double[,] mat, double degree)
{
double rad = degree *
Math.PI / 180;
double[,] rot = { {
Math.Cos(rad), -Math.Sin(rad), 0 }, { Math.Sin(rad), Math.Cos(rad), 0 }, { 0,
0, 1 } };
mat = Multiply(rot, mat);
}
public static void Magnify(ref double[,] mat, double x, double y)
{
double[,] ratio = { { x,
0, 0 }, { 0, y, 0 }, { 0, 0, 1 } };
mat = Multiply(ratio, mat);
}
public static void Translation(ref double[,] mat, double x, double y)
{
double[,] translate = { {
1, 0, x }, { 0, 1, y }, { 0, 0, 1 } };
mat = Multiply(translate, mat);
}
그림 12 Transformation 코드 일부
Multiply 함수는 두 행렬을 받은 뒤 먼저 result라는 빈 행렬을 만들어낸다. 먼저, 앞에 곱해질 행렬의 열 수와 뒤에 곱해질 행렬의 행 수가 같아 곱셈이 가능한지 확인하고 예외처리를 해 준다. 그리고 이중 for 문을 설정하여 앞에 곱해질 행렬의 행과 뒤에 곱해질 행렬의 열에 대한 곱셈을 수행할 준비를 하게 된다. 이때 i는 앞에 곱해질 행렬의 행, j는 뒤에 곱해질 행렬의 열 값을 가지고 된다. 이중 포문 내에 먼저 sum이라는 double 변수를 먼저 선언하고, 다시 for 문을 설정하여 sum에 앞에 곱해질 행렬의 행에 있던 요소와 뒤에 곱해질 행렬의 열에 있던 요소의 곱셈 결과를 차례차례 더한다. 그럼 sum은 곱해진 행렬에 들어갈 요소의 값이 되고, 이 요소의 값을 result의 알맞은 위치에 넣어 곱셈의 결과를 result에 저장한다. 이 result를 리턴 값으로 내보낸다.
Rotate 함수는 우선 degree로 받은 각도의 값을 라디안으로 변환하여 그 값을 rad에 저장한다. 이 값을 이용하여 수식 7에서 등장한 선형 사상을 계산한 뒤 행렬 rot에 저장하고, Multiply를 이용해 rad와 Input으로 받은 행렬의 곱을 계산한 뒤 다시 Input으로 받았던 행렬에 그 결과를 저장한다.
Magnify 함수는 수식 8에 등장한 선형 사상을 Input으로 받은 x와 y를 이용하여 계산한 뒤, 행렬 ratio에 저장한다. 그리고 Multiply를 이용해 ratio와 Input으로 받은 행렬의 곱을 계산한 뒤 다시 Input으로 받았던 행렬에 그 결과를 저장한다.
Translation 함수는 수식 9에 등장한 선형 사상을 Input으로 받은 x와 y를 이용하여 계산한 뒤, 행렬 translate에 저장한다. 그리고 Multiply를 이용해 translate와 Input으로 받은 행렬의 곱을 계산한 뒤 다시 Input으로 받았던 행렬에 그 결과를 저장한다.
public static double Det(double[,] mat)
{
double det = 0;
double[,] smat = new double[mat.GetLength(0)-1,
mat.GetLength(1)-1];
if (mat.GetLength(1)
== 2)
{
det = (mat[0, 0] * mat[1, 1]) -
(mat[1, 0] * mat[0, 1]);
}
else
{
for (int i = 0; i <
mat.GetLength(1); i++)
{
for (int j = 1; j < mat.GetLength(0);
j++)
{
for (int k = 0; k < i;
k++)
{
smat[j - 1, k] =
mat[j, k];
}
for (int k = i + 1; k <
mat.GetLength(0); k++)
{
smat[j - 1, k - 1]
= mat[j, k];
}
}
if (i % 2 == 0)
{
det += mat[0,i]*Det(smat);
}
else
{
det -= mat[0, i] *
Det(smat);
}
}
}
return det;
}
그림 13 Det 함수에 관한 코드
이 함수는 재귀함수의 형태를 띠는데, 우선 행렬의 열 수가 2일 때는 Background에서 보여준 2x2 행렬의 행렬식 값을, 즉 Input으로 받은 행렬의 행렬식 값을 계산하여 리턴 값으로 내보내게 된다. 만약 그 이상이라면 삼중 for문을 설정하게 되는데, 이 삼중 for문은 for문 내의 이중 for문으로 구성된 형태를 띠고 있다. Background를 참고하면, for문은 행렬의 첫째 행의 요소들을 차례차례 선택하는 역할을 하며, (i는 선택된 요소의 열 위치가 된다) 그 for문 내의 이중 for문은 각 요소에 해당되는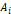 
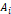를 smat라는 앞서 설정된 빈 행렬에 저장하는 역할을 한다. 이중 for문 중 내부 for문이 두 개로 구성되어서 Background의 그림 1 중 파란색 부분을 합치고 있는 것을 코드에서 확인할 수 있다. smat 계산 후에는 i가 짝수인지 홀수인지 확인하여 짝수이면 선택된 요소와 smat의 행렬식의 곱을 det에 더하고, 홀수이면 빼는 것을 코드에서 확인할 수 있다. 이렇게 하면 함수는 재귀 함수가 되어 Input으로 받는 행렬의 크기가 2x2가 될 때까지 계속 ‘재귀’하는 모습을 볼 수 있게 된다. 결과적으로 for문이 끝난 뒤 det에는 전체 행렬의 행렬식 값이 저장되며, 함수는 이 저장된 값을 리턴 값으로 반환한다.
를 smat라는 앞서 설정된 빈 행렬에 저장하는 역할을 한다. 이중 for문 중 내부 for문이 두 개로 구성되어서 Background의 그림 1 중 파란색 부분을 합치고 있는 것을 코드에서 확인할 수 있다. smat 계산 후에는 i가 짝수인지 홀수인지 확인하여 짝수이면 선택된 요소와 smat의 행렬식의 곱을 det에 더하고, 홀수이면 빼는 것을 코드에서 확인할 수 있다. 이렇게 하면 함수는 재귀 함수가 되어 Input으로 받는 행렬의 크기가 2x2가 될 때까지 계속 ‘재귀’하는 모습을 볼 수 있게 된다. 결과적으로 for문이 끝난 뒤 det에는 전체 행렬의 행렬식 값이 저장되며, 함수는 이 저장된 값을 리턴 값으로 반환한다.
public static void Transpose(ref double[,] mat)
{
double[,] temp = new double[mat.GetLength(0),mat.GetLength(1)];
System.Array.Clear(temp, 0,
temp.Length);
for (int i = 0; i <
mat.GetLength(0); i++)
{
for (int j = 0; j <
mat.GetLength(1); j++)
{
temp[i, j] = mat[i, j];
}
}
for (int i = 0; i <
mat.GetLength(0); i++)
{
for (int j = 0; j <
mat.GetLength(1); j++)
{
mat[j, i] = temp[i, j];
}
}
}
그림 14 Transpose 함수에 관한 코드
Transpose는 우선 temp라는 Input으로 받는 행렬과 같은 크기를 가지는 빈 행렬을 선언하고, 그 요소를 0으로 전부 초기화 시킨다. 그리고 이중 for문을 통해 Input으로 받는 mat 행렬의 요소들을 전부 동일하게 옮겨 놓는다. 그리고 다시 이중 for문을 통해 mat[j,i]에 temp[I,j]의 값들을 저장함으로써, mat에 temp의 전치행렬, 즉 과거의 mat의 전치 행렬을 저장하게 된다.
public static double[,] GetMap(double[,] x, double[,] y)
{
double[,] result = new double[y.GetLength(0),
x.GetLength(1)];
double[,] smat = new double[y.GetUpperBound(0),
x.GetUpperBound(1)];
double det = Det(x);
for(int i = 0; i <=
result.GetUpperBound(0); i++)
{
for(int j = 0; j <=
result.GetUpperBound(1); j++)
{
for(int k = 0; k < i; k++)
{
for(int w = 0; w < j;
w++)
{
smat[k, w] = x[k,
w];
}
for(int w = j+1; w <=
result.GetUpperBound(1); w++)
{
smat[k, w - 1] =
x[k, w];
}
}
for(int k = i+1; k <= result.GetUpperBound(0);
k++)
{
for (int w = 0; w < j;
w++)
{
smat[k - 1, w] =
x[k, w];
}
for (int w = j + 1; w <= result.GetUpperBound(1);
w++)
{
smat[k - 1, w - 1]
= x[k, w];
}
}
result[i, j] = Det(smat);
}
}
그림 15 GetMap 함수에 관한 코드 1
우선 리턴 값으로 내놓을 result라는 빈 행렬을 선언하는데, 그 행의 수는 Input으로 받은 y의 행의 수와 같도록 하고, 열의 수는 x의 열 수와 같도록 한다. 그리고 smat라는 빈 행렬을 선언하는데, 그 행과 열의 수는 result보다 1 작은 수가 되도록 한다. det라는 double 변수 또한 선언하고, 이에는 x의 행렬식 값을 저장한다. 그 다음에는 사중 for문이 오는데, 이는 이중 for문 내부의 이중 for문 구조로 이루어져 있다. 외부의 이중 for 문은 Background의 그림 2에서 볼 수 있는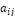 
를 차례차례 선택하는 과정이며, 그 내부의 이중 for 문 중 첫째 이중 for문은 이에 대응하는 행렬 
를 구하는 과정이다. 그림 2의 파란색 부분을 합치는 과정처럼 이중 for문이 행렬을 구하면, 그 결과를 smat에 저장한다. 둘째 이중 for문은 그 다음에 smat에 저장된 행렬의 행렬식을 구하고, result 행렬의 자리 
에 행렬식을 집어넣는 역할을 한다.
를 차례차례 선택하는 과정이며, 그 내부의 이중 for 문 중 첫째 이중 for문은 이에 대응하는 행렬 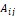를 구하는 과정이다. 그림 2의 파란색 부분을 합치는 과정처럼 이중 for문이 행렬을 구하면, 그 결과를 smat에 저장한다. 둘째 이중 for문은 그 다음에 smat에 저장된 행렬의 행렬식을 구하고, result 행렬의 자리 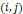에 행렬식을 집어넣는 역할을 한다.
Transpose(ref result);
for(int i = 0; i <=
result.GetUpperBound(0); i++)
{
for(int j = 0; j <=
result.GetUpperBound(1); j++)
{
if((i+j) % 2 == 0)
{
result[i, j] =
result[i, j] / det;
}
else
{
result[i, j] = (-1) *
result[i, j] / det;
}
}
}
result = Multiply(y, result);
return result;
}
}
그림 15 GetMap 함수에 관한 코드 2
그 다음, Transpose 함수를 통해 result의 전치행렬을 다시 result에 저장한다. 그리고 이중 for문을 통해 요소 중 자리잡은 행 위치(i+1)와 열 위치(j+1)의 합이 짝수인 것은 그 요소를 det로 나눈 값을 그 요소의 위치에 대입하고, 홀수 인 것은 그 요소를 -det로 나눈 값을 그 요소의 위치에 대입한다. 그러면 result에는 행렬 x의 역행렬이 저장된다. 하지만 구하고자 하는 행렬은 사상 행렬이므로, y에 result, 즉 x의 역행렬을 곱한 행렬을 다시 result에 저장한 뒤, return을 리턴 값으로 넘겨주게 된다.
static void Main(string[] args)
{
double[,] pos = { { 100,
100 }, { 200, 100 }, { 100, 200 } };
Triangle tri = new Triangle(pos);
tri.Draw("output1.ps");
Transformation.Rotate(ref tri.mat, 10);
tri.Draw("output2.ps");
Transformation.Magnify(ref tri.mat, 2, 3);
tri.Draw("output3.ps");
Transformation.Translation(ref tri.mat, 50, -50);
tri.Draw("output4.ps");
double[,] pos2 = { { 150,
150 }, { 300, 200 }, { 50, 300 } };
tri = new Triangle(pos);
Triangle tri2 = new Triangle(pos2);
double[,] result =
Transformation.GetMap(tri.mat, tri2.mat);
for(int i = 0; i <= result.GetUpperBound(0); i++)
{
for(int j = 0; j < result.GetLength(1); j++)
{
Console.Write("{0}\t", result[i, j]);
}
Console.WriteLine();
}
}
그림 16 Main 함수에 관한 코드
문제 조건에서 지시된 삼각형의 좌표 중 원래 Domain 좌표에 해당하는 것을 pos에 저장한다. Triangle을 새로 선언하고(tri), pos를 Input으로 넣는다. 그리고 변환 전 원래 모습의 삼각형을 output1.ps에 그리고, 회전 후의 삼각형을 output2.ps에, 확대 후의 삼각형을 output3.ps에, 평행이동 후의 삼각형을 output4.ps에 그린다. 이번엔 PostScript 좌표에 해당하는 삼각형의 좌표를 pos2에 저장하고, pos1을 pos2로 변환하는 사상을 Transformation 클래스 중 GetMap 함수로 구한 뒤, 그 결과 값을 이중 for 문을 통해 출력한다.
class Triangle
{
public double[,] mat = { { 0, 0,
0 }, { 0, 0, 0 }, { 1, 1, 1 } };
public Triangle()
{
}
public Triangle (double[,] pos)
{
for(int i = 0; i < 3;
i++)
{
for(int j = 0; j < 2;
j++)
{
this.mat[j, i] = pos[i,
j];
}
this.mat[2, i] = 1;
}
}
public void Draw(string fileName)
{
StreamWriter sw = new
StreamWriter(fileName);
sw.WriteLine("newpath");
sw.WriteLine("{0} {1}
moveto", mat[0, 0], mat[1, 0]);
sw.WriteLine("{0} {1}
lineto", mat[0, 1], mat[1, 1]);
sw.WriteLine("{0} {1}
lineto", mat[0, 2], mat[1, 2]);
sw.WriteLine("{0} {1}
lineto", mat[0, 0], mat[1, 0]);
sw.WriteLine("closepath");
sw.WriteLine("stroke");
sw.Close();
}
}
그림 17 Trianlge 클래스의 코드
행렬 mat를 선언하는데, 이 행렬에는 수식 4에서 등장한 행렬이 저장되어야 한다. Triangle 선언 시에, 받았던 행렬 pos가 수식 4에서 등장한 행렬의 형태가 되도록 보정된 결과가 mat에 저장되게 된다.
Draw 함수에서는 StreamWriter를 통해 받은 파일 경로에 PostScript 파일을 그리게 된다. mat의 요소를 잘 골라내어 PostScript 파일을 그리게 된다.
III. Result
우선, 콘솔 창에 출력된 결과는 다음과 같다.
그림 18 콘솔 창 출력 결과
변환 사상이 출력이 되는데, 이 답이 맞는지 확인해보기 위해서 WolframAlpha로 계산한 결과와 비교해보았다.
그림 19 WolframAlpha 출력 결과
콘솔 창에서 출력이 된 결과와 동일함을 알 수 있다.
그리고 다음은 출력된 PostScript 파일의 결과들이다.
그림 20 변환되지 않은 삼각형
그림 21 회전 후의 삼각형
그림 22 확대 후의 삼각형
그림 23 평행이동 후의 삼각형
화면의 왼쪽 아래 가장자리가 원점이고, 아래쪽 한계선이 
축, 왼쪽 한계선이 
축인데, 이를 토대로 보았을 때 모두 적절하게 출력되는 모습을 볼 수 있다.
축, 왼쪽 한계선이 축인데, 이를 토대로 보았을 때 모두 적절하게 출력되는 모습을 볼 수 있다.