[서울대 물리학실험 2-4] 전자기 이끎

물리학실험 2-4

2-4. 전자기 이끎

*본 보고서는 이미 제출된 적 있는 보고서로 표절 시 발각될 확률이 높으니 참고만 해주십시오.

참고: http://physlab.snu.ac.kr/documents/manual/2017-2/Ko/2-4%20%ED%95%9C%EA%B8%80.pdf

1. Introduction

1.1. 실험 목적

이 실험을 통해 전자기 이끎이 존재함을 확인하고, 자기 마당 내부에서 도선 고리가 회전할 때 발생하는 기전력을 조사하여 전자기 이끎 현상을 정량적으로 조사한다. 이것을 통해 전동기의 원리에 대해서도 이해한다.

1.2. 배경 지식

1.2.1. 교류 기전력의 발생

단면적이 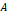이고, 감긴 수가 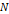회인 도선 고리가 자속 밀도가 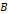로 일정한 곳에서 일정한 각속도 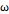로 돌고 있을 때, 고리의 단면에 수직한 선이 자기마당과 이루는 각도 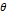를 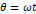라고 쓸 수 있다면, 고리면을 지나는 자기 선속에 대하여

위와 같이 쓸 수 있으며, 유도 기전력 에 대해,

위에서 구한 자기 선속의 공식을 적용하면,

1.2.2. 직류 기전력의 발생

그림 1 직류 전동기

그림 2의 전동기는 두 개의 고리가 직각을 이루고 있다. 그러므로 브러쉬에 의해 발생한 기전력의 크기가 큰 때민 서로 교대하며 기전력을 제공하게 되어 있다. 회전 주기가 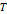이고, 각속도가 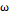이며, 초기 전압이 인 전동기를 돌렸을 때 발생하는 출력 전압에 대해,

파형을 보면 진동기의 회전수보다 4배의 떨기 수를 가지고 있음을 알 수 있다.

또, 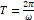임을 이용하여 평균 전압을 계산하면,

또한, 최소 전압은 이 된다.

1.3. 실험 안내

솔레노이드 (500회), 영구 막대 자석, 멀티 테스터, 패러데이 실험장치 (300회), 1채널 직류 전원 장치, 연결 도선, Hantek 오실로스코프, BNC 케이블, USB 케이블을 준비한다.

1.3.1. 전동기를 통해 유도되는 DC 전압 측정

① 실험 장치의 DC 단자로 바꾸어 오실로스코프와 연결해 준다.

② 영구 자석을 정방향으로 두고, 파워 서플라이로 전압을 주며 출력되는 유도 기전력의 형태와 크기를 관측한다.

③ 파워 서플라이의 전압을 크게 하면서 유도 기전력의 변화를 관측한다.

④ 영구 자석을 다른 형태로 바꾸어 실험한다.

1.3.2. 전동기를 통해 유도되는 AC 전압 측정

① 실험 장치의 AC 단자로 바꾸어 오실로스코프와 연결한다.

② 나머지 과정은 1.3.2와 마찬가지로 진행한다.

2. Data & Result

영구 자석의 크기를 설정한 뒤, AC와 DC 단자에 각각 연결하고 걸어 준 전압의 크기를 변화시켰을 때 그래프의 개형이 어떻게 그려지는지 확인하였다.

2.1. 자석에 따른 그래프의 개형

다음은 영구 자석의 크기가 충분히 크고 걸어준 전압의 크기가 9.4V인 경우, 교류 기전력이 발생했을 때 유도 기전력에 대한 그래프와 직류 기전력이 발생했을 때 유도 기전력에 대한 그래프이다.

그림 2 영구자석의 크기가 큰 경우(위:AC, 아래:DC)

AC 그래프는 어느 정도 사인 또는 코사인 함수의 모습을 비슷하게 나마 따르고 있고, DC 그래프는 AC 그래프의 값에 절댓값을 씌운 것과 같은 형태를 가지고 있다.

반면, 영구자석의 크기가 충분하지 않은 크기를 가진 경우, 그래프의 개형은 다음과 같았다. 위는 AC, 아래는 DC 기전력이다. (걸어준 전압: 9.4V)

그림 3 영구 자석의 크기가 충분히 크지 않은 경우

자석의 크기가 어느 정도 컸을 때는 AC 그래프의 개형이 sin 함수를 일정 부분 따라갔던 반면, 영구 자석의 크기가 고리의 크기만큼 충분히 크지 않은 경우, 그래프의 개형이 1.2.1에서 예상한 것에서 많이 벗어나 있는 것을 확인할 수 있다. 또, 아래의 그림은 영구 자석의 크기가 매우 작을 때 그려지는 AC 그래프로, 걸어 준 전압은 8.8V이다.

그림 4 영구 자석의 크기가 작은 경우

그래프의 개형이 예상된 형태에서 더욱 많이 벗어나 있는 것을 확인할 수 있다. 이의 이유는 고리가 속해 있는 자기마당의 자속밀도가 일정하지 않다는 것에 있다. 자석의 크기가 크면 자기마당 자속밀도가 일정한 것과 같은 효과를 보게 되는데, 그림 3이나 그림 4과 같이 영구 자석의 크기가 충분히 크지 못할 경우, 자속밀도의 일정한 정도가 떨어지며 그래프의 개형이 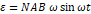를 만족하는 형태에서 벗어나게 되는 것이다. 배경 지식에서 가정했던 것과 같이 각속도 등등이 일정하지 않고, 고리가 회전하는 도중 변화하는 것을 그림 3과 4, 그리고 조금이나마 그림 2에서도 확인할 수 있다.

2.2. AC와 DC 그래프의 차이

그림 2나 그림 3을 보면, DC의 그래프는 AC의 그래프 중에서 t-축 아래에 있는 부분을 t-축에 대해 대칭이동 시킨 것과 같은 형태를 가지고 있는 것을 확인할 수 있었다. 특히, 기계 오작동이 일어나지 않아 정확한 결과가 나온 그림 3의 경우, 그래프의 진폭까지 완벽하게 일치한 것까지 확인할 수 있었다. 이것은 1.2.2에서 본 두 개의 고리가 직각을 이루고 있는 전동기가 아니라 고리 한 개로만 이루어진 직류 전동기에서 볼 수 있는 형태에 훨씬 더 가깝다.

고리가 한 개로만 이루어진 전동기에서 그림 2, 3 같은 결과가 나오는 이유는 바로 브러쉬의 교차 때문이다. AC 단자의 경우, 브러쉬가 없어 반 바퀴 돌아가면 전류의 방향도 반대로 바뀌지만, 브러쉬가 있는 DC 단자를 이용하면 전류의 방향이 바뀌는 것을 줄일 수 있는 것이다.

2.3. 공식의 정량적 확인

1.2.1의 공식인 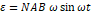를 확인하기 위해서는 자속밀도의 일정한 정도가 일정 수준 이상인 환경에서 진행된 실험 결과를 이용할 필요가 있다. 그러므로 크기가 큰 영구자석을 이용해서 진행한 실험 결과만을 이용하여 이론을 확인하도록 한다. 다만, AC 단자에 연결하여 실험을 진행하던 도중 기계가 오작동을 보여 제 성능을 온전히 내지 못한 점을 감안해야 한다.

기전력의 진폭을 각속도로 나눈 값은 이론적으로 로, 이론이 타당하다면 실험 결과에서 기전력의 진폭을 각속도로 나눈 값은 모든 전압에서 일정해야 한다. 다음은 이를 나타내는 그래프이다.

그림 5 DC 기전력에서 NAB

그림 6 AC 기전력에서 NAB

어느 정도 일정한 값을 보이는 것을 그래프를 통해 확인할 수 있다. DC에서 NAB에 대한 표준편차는 0.000103122, AC에서 NAB에 대한 표준편차는 0.000593495로, 매우 작은 값이었다.

2.4. 파워 서플라이 전압에 따른 각속도 변화

파워 서플라이로 가해주는 전압 크기의 변화에 따라 각속도가 어떻게 변화하는지 그래프로 나타냈다. 다음은 AC 기전력에 대한 그래프와 DC 기전력에 대한 그래프이다.

그림 7 AC 기전력의 경우 각속도의 변화

그림 8 DC 기전력의 경우 각속도 변화

파워 서플라이로 가해주는 전압이 증가하면, 고리가 회전하는 각속도 또한 선형적으로 증가한다는 것을 볼 수 있었다. 추세선에 대한 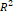또한 0.985 이상으로 상당히 높은 값으로, 전압과 각속도 사이의 선형 관계를 보여주기 충분한 값이다.

각속도는 선형적으로 증가하고 NAB의 값은 이론적으로 일정하므로, 기전력의 진폭 또한 선형적으로 증가하는 결과를 보일 것이다. 다음은 이에 대한 그래프이다.

그림 9 AC 기전력의 경우 기전력 진폭의 변화

그림 10 DC 기전력의 경우 기전력 진폭의 변화

3. Discussion

실험 과정에서 제대로 통제하지 못한 요인이 무엇인지, 그리고 이 요인으로 인해 발생한 오차가  결과의 해석에 어떠한 영향을 미치는지 논의한다.

3.1. 기계의 오작동

크기가 큰 영구자석을 이용하여 AC 기전력을 측정할 당시 패러데이 장치의 모터가 제대로 돌아가지 않는 등 오작동을 보였다. 각속도의 비율은 그대로였으나, 각속도의 크기 자체는 현저히 감소했다. AC의 기전력 진폭과 DC의 기전력 진폭을 비교할 때 크기가 큰 영구자석을 이용하여 진행한 실험 자료는 어느 정도 배제하는 등 오작동을 고려하여 실험 자료를 해석하였다.

3.2. 자속밀도의 일정한 정도

이론에서는 도선 고리(코일)이 있는 자기마당의 자속밀도가 일정하다고 가정하고 공식을 세웠으나, 실제로 크기가 큰 영구자석에서도 이러한 가정은 엄밀하게 성립하지 않았다. 이로 인해 그래프 결과가 1.2의 공식에 부합하지 않을 수 있었음을 실험 결과 분석 도중 고려하였다.

3.3. 측정 한계

파워 서플라이로 걸어준 전압의 값을 측정하거나 기전력의 값을 측정할 때, 기계의 측정 성능 한계로 인하여 실험 데이터에 오차가 생겼을 수 있다. 파워 서플라이 전압의 최소 단위가 0.1V였기 때문에, 그림 5 ~ 10의 그래프에 0.05V의 오차막대를 삽입하였다. 또한, 그림 2 ~ 4를 보았을 때, 유도 기전력의 값에 대해서도 최소 5%의 오차율을 가지게 됨을 알 수 있으며, 이 오차율 또한 오차막대의 형태로 그림 5 ~ 10의 그래프에 삽입하였다.

위와 같은 오차를 고려하더라도, 이 오차가 상대적으로 매우 작기 때문에 실험 결과의 해석에 별다르게 큰 변화를 주지는 못할 것이라고 말할 수 있을 것이다.

4. Conclusion

이 실험을 통해 유도 기전력에 대한 이론을 정량적으로 확인해 보았다.

첫 번째로, 자석에 따른 유도 기전력 그래프의 개형을 확인해 보았다. 자석의 크기가 고리의 크기만큼 큰 경우에는 그래프의 개형이 sin 또는 cos 함수의 개형을 비슷하게 따라갔으나, 자석의 크기가 고리의 크기에 비해 상대적으로 작은 경우에는 개형이 sin 또는 cos 함수의 형태에서 어긋나는 것을 관찰할 수 있었다. 이는 자석의 크기가 클수록 고리가 속해 있는 자기마당의 자속밀도가 더욱 일정해 보여서, 1.2에서 내린 가정(자속밀도가 일정함)을 더욱 충실히 따라갔기 때문인 것으로 예측할 수 있었다.

두 번째로, AC와 DC 기전력에서 그래프의 개형이 어떻게 차이나는 지를 보았다. DC 기전력의 그래프는 AC 기전력에 절댓값을 씌운 함수의 개형을 어느 정도 따르고 있었다. 이러한 형태는 실험 과정에서 사용한 영구 자석의 크기가 큰 경우 뚜렷하게 드러났다. 영구 자석의 크기가 충분히 크지 않은 경우에는 AC 기전력에 절댓값을 씌운 형태를 엄밀히 따라가지는 않고 조금 더 복잡한 형태를 띠고 있었으나, 그래도 어느 정도 따라가는 모습을 볼 수 있었다. 이러한 모습은 고리가 2개 달린 직류 전동기보다는 고리가 1개 달린 직류 전동기에서 볼 수 있는 기전력의 형태에 가까웠다.

세 번째로, 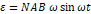라는 공식의 정량적인 확인을 진행하였다. 우선, 기전력에 대한 그래프에서 진폭의 값을 각속도로 나눈 값이 이론에서 예측할 수 있는 것처럼 일정한지를 확인해 보았다. 그래프를 그리고 표준편차의 값을 구해서 확인해 본 결과, 실험적으로도 그 값이 일정하다고 말할 수 있었다.

네 번째로, 파워 서플라이로 걸어 준 전압 값이 변화할 때 기전력의 진폭이 어떻게 변화하는지 확인해 보았다. 우선, 기전력의 진폭과 관계가 깊은 도선 고리의 회전 각속도의 값이 파워 서플라이로 걸어 준 전압 값에 따라 어떻게 변화하는지 보았다. 파워 서플라이로 걸어 준 전압의 값이 일정한 속도로 증가할 때 각속도 또한 일정한 속도로 증가하였다. 즉 파워 서플라이 전압 값과 각속도의 값이 선형적인 관계를 가지고 있음을 볼 수 있었다. 마찬가지로 기전력의 진폭 또한 파워 서플라이의 전압 값이 일정한 속도로 증가하면 함께 일정한 속도로 증가하는 모습을 볼 수 있었다.

이러한 결과를 도출해낸 실험에서도 통제 불가능한 요인 때문에 실험 데이터에 오차가 발생한 모습을 볼 수 있었다. 이러한 요인으로는 기계의 오작동, 영구 자석의 충분하지 못한 크기(자속밀도의 일정한 정도), 실험 장치의 측정 성능 한계 등이 있었다. 하지만 이러한 요인으로 발생한 오차는 실험 결과를 해석하는데 있어서 별 무리를 주지 않았다.

이러한 통제 불가능한 요인을 최소화하고 실험 결과의 해석을 용이하게 하기 위해서는 다음과 같은 일을 할 수 있겠다. 우선, 영구 자석의 크기를 늘린다. 영구 자석이 크면 클수록 자기마당의 자속밀도가 더욱 일정해 보이는 효과를 낼 수 있을 것이다. 이는 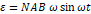의 공식을 확인하기 쉽게 만들어 준다. 또한, 열에 취약하지 않고 고장 나기 쉽지 않은 모터와 도선 고리를 사용해야 한다. 고리의 각속도가 일정해 보이는 효과를 내기 위해서는 각속도가 어느 정도 크기를 가져야 하는데 실험에 쓰인 장치가 약해서 이를 시행할 수 없었다. 이 점을 개선한다면 실험의 결과를 해석하기 훨씬 더 수월할 것이다.

*Reference

1 <2-4. 전자기 이끎>, 《Physics Laboratory》, 서울대학교 물리천문학부 편, 2017.