Programming Assignment #02
*본 보고서는 이미 제출된 적 있는 보고서로 표절 시 불이익을 받을 수 있습니다. 참고용으로만 활용하세요.
<제목 차례>
I. Introduction
1. Problem
2. Conditions
II. Programming
1. Input(s)
2. Output(s)
3. Procedure
4. Detailed Description
III. Result
IV. Discussion
<표 차례>
표 1 프로그램 전체에 대한 Input(s)
표 2 ComputeFunction 함수에 대한 Input(s)
표 3 tri_avg 함수에 대한 Input(s)
표 4 dvol 함수에 대한 Input(s)
표 5 프로그램 전체에 대한 Output(s)
표 6 ComputeFunction 함수에 대한 Output(s)
표 7 tri_avg 함수에 대한 Output(s)
표 8 dvol 함수에 대한 Output(s)
<그림 차례>
그림 1 체적의 산출
그림 2 Main 함수에 대한 알고리즘 순서도
그림 3 ComputeFunction 순서도
그림 4 tri_avg 순서도
그림 5 dvol 순서도
그림 6 Code 파편 1
그림 7 Code 파편 2
그림 8 Code 파편 3
그림 9 Code 파편 4
그림 10 Code 파편 5
그림 11 결과물
<수식 차례>
수식 1 단위 부피를 구하는 식
I. Introduction
1. Problem
구분구적법을 이용하여 다음 결과 값을 구해 콘솔 창에 출력하라.
2. Conditions
이는 프로그래밍을 할 때 만족시켜야 할 조건이다.
① C#으로 코딩을 해야 한다.
② 
방향 모두 동일한 개수의 구간으로 나눠야 하며, 그 구간의 수는 콘솔을 통해 입력하도록 한다.
방향 모두 동일한 개수의 구간으로 나눠야 하며, 그 구간의 수는 콘솔을 통해 입력하도록 한다.
③ 함수 값과 단위 부피를 계산하는 데에 Main 함수 외부에 있는 함수를 이용하도록 한다.
④ 계산된 함수 값은 2차원 배열에 저장하도록 한다.
II. Programming
1. Input(s)
Input(s)
|
Type
|
설명
|
n
|
int
|
적분 구간(구분구적 구간)의 분할 수
|
표 1 프로그램 전체에서의 Input(s)
Input(s)
|
Type
|
설명
|
x
|
double
|
함수의 값을 얻기 위해 대입할 x좌표를 나타냄.
|
y
|
double
|
함수의 값을 얻기 위해 대입할 y좌표를 나타냄.
|
표 2 ComputeFunction 함수에 대한 Input(s)
Input(s)
|
Type
|
설명
|
x
|
double
|
평균을 구하기 위한 첫째 값
|
y
|
double
|
평균을 구하기 위한 둘째 값
|
z
|
double
|
평균을 구하기 위한 셋째 값
|
표 3 tri_avg 함수에 대한 Input(s)
Input(s)
|
Type
|
설명
|
f1
|
double
|
단위 입체 밑면 중 x와 y좌표가 가장 작은 위치의 함수 값
|
f2
|
double
|
밑면에서 f1위치보다 x나 y좌표 중 하나만 큰 곳의 함수값
|
f3
|
double
|
밑면에서 f1위치보다 x나 y좌표 중 하나만 큰 곳의 함수값
|
f4
|
double
|
단위 입체 밑면 중 x와 y좌표가 가장 큰 위치의 함수 값
|
interval
|
double
|
쪼갠 적분 구간 중 한 구간의 길이
|
표 4 dvol 함수에 대한 Input(s)
2. Output(s)
Output(s)
|
Type
|
설명
|
sum
|
double
|
구분구적법을 이용하여 계산해낸 수치적 적분의 값
|
표 5 프로그램 전체에서의 Output(s)
Output(s)
|
Type
|
설명
|
함수의 리턴 값
|
double
|
주어진 (x,y)에 대한 함수 값
|
표 6 ComputeFunction 함수에 대한 Output(s)
Output(s)
|
Type
|
설명
|
함수의 리턴 값
|
double
|
주어진 세 값에 대한 평균
|
표 7 tri_avg 함수에 대한 Output(s)
Output(s)
|
Type
|
설명
|
함수의 리턴 값
|
double
|
주어진 값을 통해 계산한 단위 부피
|
표 8 dvol 함수에 대한 Output(s)
3. Procedure
적분 구간을 나눈 뒤에 단위 부피를 합하는 방식으로 수치적 적분 값을 산출할 것이다.
그림 1 체적의 산출
적분 구간을 쪼갤 때, 그 단위 구간의 길이를 
라고 하자. 단위 부피를 계산하기 위해 그림 1에서와 같이 삼각기둥 두 개의 합을 이용하게 되는데, 이렇게 계산하게 되면 그 부피는 다음과 같다.
라고 하자. 단위 부피를 계산하기 위해 그림 1에서와 같이 삼각기둥 두 개의 합을 이용하게 되는데, 이렇게 계산하게 되면 그 부피는 다음과 같다.
수식 1 단위 부피를 구하는 식
다음과 같은 단위 부피들의 합을 구해서 수치적 적분 값을 구하게 되는데, 단위 구간의 길이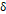 
가 작으면 작을수록, 즉 적분 구간을 많이 쪼개면 쪼갤수록 산출한 값은 실제 적분 값과의 오차를 작게 가지게 된다.
가 작으면 작을수록, 즉 적분 구간을 많이 쪼개면 쪼갤수록 산출한 값은 실제 적분 값과의 오차를 작게 가지게 된다.
그림 2 Main 함수의 알고리즘 순서도
처음에 구간을 몇 개로 나눌 지 결정하기 위해 n 값을 입력하게 한다. n의 값을 이용해서 단위 구간의 길이 intval을 결정짓고, tempx와 tempy를 각각 이용해서 function_value에 (tempx, tempy)에 해당하는 함수 값을 저장한다. 그리고 상술한 방법으로 단위 부피를 계산하는 dvol 함수를 이용하는데, sum에 dvol이 리턴한 값을 계속해서 더해 나간다. 마지막으로 sum을 출력하고, 이를 실제 적분 값과 비교할 수 있도록 한다.
ComputeFunction 함수는 x와 y에 대해 (x, y)에 대응하는 f(x,y) 값을 반환하며, tri_avg 함수는 주어진 세 실수의 평균을 반환하고, dvol 함수는 주어진 함수 값 4개와 단위 구간의 길이를 이용하여 단위 부피를 계산하고 그 값을 반환한다.
그림 3 ComputeFunction 순서도
그림 4 tri_avg 순서도
그림 5 dvol 순서도
4. Detailed Description
Main 함수에 대해서 먼저 살펴볼 것이다. 우선, 적분 구간을 몇 개로 쪼갤 것인지 물어보고, n의 값을 정한다. 이때, x축과 y축이 각각 n개의 구간으로 나뉘게 되는데, 구간의 시작점부터 세면 x축과 y축 각각 (n+1)개의 지점을 갖게 되므로, function_value의 행과 열은 n+1이 돼야 한다. 단위 구간의 길이의 뜻을 가지는 intval의 경우, 10/n을 값으로 가지게 된다. tempx와 tempy는 함수 값을 계산하여 function_value에 저장할 때 쓸 x좌표와 y좌표를 가지게 되는데, x좌표와 y좌표 모두 시작점이 -5여야 하므로 tempx와 tempy 모두 초기값을 -5로 설정하게 된다. 또, sum은 초기값을 0으로 설정한다.
Console.WriteLine("몇 개의 구간으로 나누실 건가요?");
int n = Convert.ToInt32(Console.ReadLine());
double[,] function_value = new double[n + 1, n + 1];
double intval = 10 / (double) n;
double tempx = -5;
double tempy = -5;
double sum = 0;
그림 6 Code 파편 1
이제는 함수 값을 function_value 배열에 저장해야 한다. 행을 x축, 열을 y축으로 대응시켜 저장할 것이다. 이중 for 문을 이용할 것인데, 겉의 for 문은 i를 증가시킬 것이고, 안의 for 문은 j를 증가시킬 것이다. 배열을 저장할 때 0, 1, 2, 3 과 같이 0에서부터 시작되어 저장하므로, 저장을 용이하게 하기 위해 i와 j 모두 초기값을 0으로 설정해 둔다. j가 1씩 증가하며 안의 for문이 실행될 때마다 (tempx, tempy)에 대응되는 함수 값이 function_value[i, j]로 저장되고, tempy는 intval 값만큼 증가하게 된다. 열의 개수가 n+1개이므로, 안의 for 문은 j <= n 일 때까지 실행되고 종료된다. 그러면 tempx는 intval 값만큼 증가하고, tempy는 다시 -5가 되며, 겉의 for문이 다시 반복을 일으키게 된다. i<=n일 때까지 실행되고 종료된다.
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
function_value[i, j] = ComputeFunction(tempx, tempy);
tempy += intval;
}
tempx += intval;
tempy = -5;
}
그림 7 Code 파편 2
이제는 sum에 단위 부피들의 값을 차례차례 더해 나가야 한다. 이중 for문을 이용해서 function_value 배열에 저장돼 있는 값을 차례차례 부르고, 그 값들을 이용해서 계산한 단위 부피를 꾸준히 sum 값에 더하게 된다. 값 i가 n-1에 다다르면 모든 값을 부르게 되므로 for문이 종료된다.
for(int i = 0; i <= n-1; i++)
{
for (int j = 0; j <= n - 1; j++)
{
sum += dvol(function_value[i, j], function_value[i + 1, j], function_value[i, j + 1], function_value[i + 1, j + 1], intval);
}
}
그림 8 Code 파편 3
이제 sum의 값을 출력하고, 실제 적분 값을 구해서 이와 비교해본다.
Console.WriteLine("구분구적법으로 구한 값:{0}", sum);
Console.WriteLine("실제로 구한 값은 약 9266.67");
그림 9 Code 파편 4
나머지는 Main 함수에서 불러온 함수에 관한 설명이다. ComputeFunction은 주어진 x, y 값에 대해, (x, y)에 대응하는 f(x, y)의 값을 리턴하는 함수이다. tri_avg는 주어진 x, y, z 값의 평균을 리턴하는 함수이며, dvol은 주어진 값들로 그림 1과 수식 1처럼 단위 부피를 계산하여 그 값을 리턴하는 함수이다.
static double ComputeFunction(double x, double y)
{
return (4 * x * x) + (7 * y * y) + (3 * x * y) + x + y + 1;
}
static double tri_avg(double x, double y, double z)
{
return (x + y + z) / 3;
}
static double dvol(double f1,double f2, double f3, double f4, double interval)
{
return 0.5 * interval * interval * (tri_avg(f1, f2, f3) + tri_avg(f2, f3, f4));
}
그림 10 Code 파편 5
III. Result
그림 11 결과물
예상한 그대로 출력되는 모습을 보여준다. 실제로 나누는 구간의 수가 많을수록 정확성이 높아지는 것을 확인할 수 있다.
IV. Discussion
구간 수가 일정 수 이상으로 넘어가게 되면 OutOfMemoryException이 발생하게 되는데, n이 일정 수 이상이면 n 값을 다시 입력하도록 하게 하는 것도 나쁘지 않은 생각인 것 같다. 또한, n을 자연수가 아닌 값(0이나 음수 등등)을 입력했을 때도 n 값을 다시 입력하도록 하게 하는 것 또한 좋은 생각인 것 같다.
