[서울대 물리학실험 2-3] 전류와 전류 사이

물리학실험 2-3

2-3. 전류와 전류 사이

*본 보고서는 이미 제출된 적 있는 보고서입니다. 표절 시 불이익을 받을 확률이 높으니 참고용으로만 쓰십시오.

참고: http://physlab.snu.ac.kr/newphyslab/lab/exp_b4.htm

1. Introduction

1.1. 실험 목적

직류 전류가 흐르는 솔레노이드의 고른 자기 마당 안에 전류가 흐르는 도선을 넣고, 이 도선이 받는 자기 돌림힘을 측정한다. 이때 돌림힘의 방향을 확인하고, 그 크기가 자기마당과 전류에 어떻게 의존하는지 확인한다.

1.2. 배경 지식

1.2.1 전류가 만드는 자기장

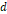전류가 만큼 흐르는 도선이 있을 때, 도선에서 만큼 떨어진 위치에 도선이 형성하는 자기장 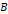에 대해 다음과 같은 식이 성립한다.

이때, 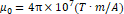이다.

또, 각각 , 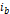의 전류가 흐르는 도선 a, b가 있을 때, 도선 b 중 의 길이만큼의 부분이 도선 a에서 주는 자기장 에 의해 받는 힘은

1.2.2 솔레노이드와 거리

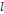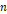길이가 , 반지름 을 가지고, 단위 길이 당 감긴 횟수가 회이며, 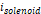의 전류가 흐르는  솔레노이드의 중심에서, 자기마당은 그 크기가

이때, 에 대해,

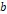전류 가 흐르는, 가로 세로의 길이가 각각 , 이며 감은 수는 1회인 고리가 자기마당 에 각도 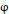만큼 기울어져 있다면, 고리가 받는 돌림힘 의 크기에 대해,

또한, 위에서 설명했던 고리가 솔레노이드 중심의 자기마당 내부에 있을 경우, 고리가 받는 돌림힘 의 크기는

1.2.3 전류 천칭

그림 1 전류 천칭 구조

고리가 받는 자기마당에 의한 힘 때문에 생기는 돌림힘을 중력에 의한 되돌림 힘이 상쇄하여 평형을 이루게 하는 것이 천칭의 원리이다.

그림 1에서와 같이 천칭의 질량이 이고, 받침대의 반지름이 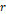이며, 받침대부터 가리키개까지의 길이가 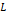, 가리키개의 수직 변위가 , 천칭이 기울어진 각도를 라고 한다면, 되돌이 돌림힘 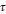의 크기는

이때, 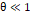이라고 가정한다면, 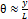이므로,

1.3. 실험 안내

① 솔레노이드를 직류 이중 전원 장치에 연결한다.

② 전류 조절 손잡이가 시계 반대로 돌려진 것을 확인하고, 전원 장치 스위치를 켠다.

③ 천칭이 위 또는 아래로 약간 기운 상태에서 솔레노이드에 닿지 않고 평형을 유지하도록 천칭에 달린 나사를 조절한다.

④ 천칭이 연결된 전원의 전류를 조절하여 전류계가 1A 정도를 가리키게 한다.

⑤ 천칭이 기울어져 있던 방향과 반대로 기울어지는지 확인하고, 만약에 그렇지 않다면 전류 방향을 바꿔서 다시 진행한다.

⑥ 전류 천칭의 전류를 0~2A 사이의 값으로 바꾸며 가리키개의 값을 기록한다.

⑦ 솔레노이드의 전류를 0~2.5A까지 바꿔가며 기록한다.

2. Data & Result

실험 환경의 요소는 다음과 같다. 전류 천칭의 질량은 19.73g이었고, 솔레노이드의 감긴 횟수는 550회였다. 솔레노이드의 길이는 12cm, 지름은 6.8cm였다. 천칭 고리의 폭은 약 29.5mm였으며, 그 고리의 감긴 횟수는 3회였다. 받침대 못의 지름은 약 1mm, 고리 끝으로부터 받침대 못까지의 거리는 약 12.5cm였다. 받침대로부터 가리키개까지의 거리는 10cm였다.

이를 토대로 2.2에 있는 공식을 통해 고리가 솔레노이드의 자기마당에 의해 받는 돌림힘을 계산하면 다음과 같다.

이때, (A)는 고리에 흐르는 전류의 크기이며, (A)는 솔레노이드에 흐르는 전류의 크기다. 그리고 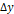(m)는 가리키개의 변위이다.

또한 중력에 의한 되돌림 돌림힘을 2.2에 있는 공식을 통해 계산해 보면,

다만 실험에서 각도는 상당히 크게 나왔기 때문에 실제로 결과값에서 이를 계산할 때에는 sin 대신에 arctan를 이용해 계산한 각도를 적용하여 실험 결과의 신뢰도를 높일 것이다.

2.1. 전류 천칭에 흐르는 전류에 따른 결과

솔레노이드에 흐르는 전류의 크기가 일정한 상태에서 전류 천칭에 흐르는 전류의 크기를 변화시켰을 때 돌림힘이 어떻게 변화하는지 관찰하였다. 그리고, 솔레노이드의 전류를 다르게 하여 이 과정을 반복하였다.

천칭이 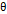만큼 기울어졌을 때, 중력에 의해 받는 천칭이 받는 되돌림힘은 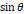에 비례하고, 천칭이 자기마당에 의해 받는 돌림힘은 와 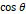에 비례하므로, 는 에 비례해야 한다. 이를 그래프로 그리어 확인하였다.

그림 2 천칭의 전류 값을 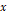축으로 했을 때 그래프

데이터를 얻어내는 과정에서 천칭이 흔들리면서 전류 값과 천칭 가리키개의 변위에 대한 오차가 생겼는데, 그 흔들린 정도를 고려하여 전류 천칭의 전류 크기에 대한 오차를 0.05A, 돌림힘의 비율(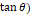에 대한 오차 범위를 10%로 주었다.

이론에 의하면, 그래프에서 솔레노이드에 흐르는 전류의 크기가 같은 점들의 분포는 원점을 지나는 직선형이어야 한다. 이를 확인하기 위하여 그래프에 추세선을 그리고 점들의 분포가 직선을 얼마나 이루는지 확인하였다. 3개의 데이터에 대한 점이 직선에서 벗어나 있는 것을 제외하고는 대체로 직선에 가까운 분포를 보이는 것을 확인할 수 있었다. 추세선에 대한 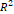의 값이 대체로 0.92 이상으로 높은 것을 통해 알 수 있다.

또, 이론에 의하면 점들이 이루는 직선의 기울기가 솔레노이드에 흐르는 전류의 크기에 비례해야 한다. 추세선의 기울기가 솔레노이드에 흐르는 전류의 크기에 따라 어떻게 변화하는지 그래프로 나타내고 그 분포가 얼마나 직선에 가까운지 확인하여 이론에 부합한 결과가 나왔는지 보았다.

그림 3 추세선의 기울기에 대한 그래프

완전한 직선이 아닌 모양을 가지긴 하지만, 이 0.86 이상으로 어느 정도 높은 값을 보이는 것을 확인할 수 있다.

2.2. 솔레노이드의 전류에 따른 결과

이번엔 의 값이 일정할 때 의 값에 따라 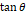의 값이 어떻게 변화하는지 확인해 보았다. 그리고 2.1에서 했던 것과 같이 값을 변화시킨 다음 이 과정을 반복하였다.

이론에 의하면 는 에 비례하므로, 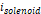에 대한 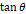의 값을 그래프로 나타낼 때, 같은 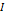값에 대한 점들의 분포는 직선형이어야 한다. 아래는 실험 결과를 토대로 그린 그래프이다.

그림 4 솔레노이드 전류에 대해 나타낸 그래프

마찬가지로 실험 결과에서 보인 결과값의 불안 정도를 고려하여 돌림힘의 비율(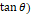에 대한 오차율은 10%로 하였고, 전류 크기에 대한 오차를 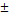0.05A로 하였다.

오차를 고려한 그래프를 통해 점들의 분포를 분석했을 때, 그 분포가 어느 정도 직선형을 띠는 것을 볼 수 있었다. 추세선에 대한 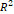의 값 또한 모두 0.82 이상으로 높았다.

또, 2.1에서 확인한 것과 마찬가지로, 이 점들이 이루는 직선의 기울기는 전류 천칭에 흐르는 전류의 크기에 비례해야 한다. 그림 4의 그래프에 그려진 추세선의 기울기가 전류 천칭의 전류 크기에 따라 어떻게 변화하는지 그래프로 나타내고, 그 분포가 얼마나 직선에 가까운지 확인하여 이론에 부합한 결과가 나왔는지 보았다.

그림 5 추세선의 기울기에 대한 그래프

거의 완전히 직선에 가까운 형태를 띠고 있는 것을 확인할 수 있었다. 의 값 또한 0.98 정도로 매우 높은 것을 확인할 수 있었다.

2.3. 이론의 정확도에 대한 확인

2의 초기 부분에서 계산한대로라면,

위와 같은 공식을 따르는 실험 결과가 나와야 이론의 정확도를 확인할 수 있다.

실험 결과가 이론에 부합한다면, 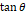를 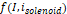라는 함수로 나타냈을 때 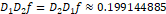이어야 하므로, 그림 3의 추세선에서 얻어낸 기울기, 그리고 그림 5의 추세선에서 얻어낸 기울기가 와 거의 같은 값이어야 한다. 그림 3의 추세선 기울기는 약 0.1954였고, 그림 5의 추세선 기울기는 약 0.2016이었으므로, 이론에 맞는 결과가 나왔다고 말할 수 있다.

3. Discussion

실험 과정에서 제대로 통제하지 못한 요인이 무엇인지, 그리고 이 요인으로 인해 발생한 오차가  결과의 해석에 어떠한 영향을 미치는지 논의한다.

3.1. 전류 천칭의 흔들림

전류의 크기가 변화하면서 힘을 받은 천칭은 단진동 운동처럼 흔들리게 되는데, 이 흔들림으로 인해 전자기 유도 현상이 발생하여 전류가 일정한 상태에서 머무르지 않고 계속 그 크기가 커졌다 작아졌다 하는 일을 겪게 된다. 이로 인해 가리키개의 변위와 전류의 크기 측정값에 꽤 큰 정도로 오차가 생겼다.

3.2. 가리키개 변위의 측정 한계

가리키개의 변위를 측정하는데 사용된 자는 작은 눈금 한 눈금당 0.2cm의 길이였다. 이는 실험 데이터에 어느 정도 오차를 발생시키기에 충분한 요인이다.

3.3. 천칭의 두께로 인한 측정 한계

천칭의 두께가 약 0.7mm 정도로 두꺼운 수준이어서 가리키개의 변위를 측정할 때 정확히 측정하는데 어려움을 겪었다. 이 또한 실험 데이터에 오차를 발생시킬 수 있다.

3.4. 지나치게 얇은 받침대 못

이론을 확인하기 위해서는 실험 요건에 대한 정확한 측정 값이 필요한데, 자 눈금에 비해 받침대 못이 지나치게 얇은 탓에 못 두께에 대한 정확한 값을 얻어내기 힘들었다. 조그만 오차조차 이론 확인에 큰 어려움을 줄 수 있었다.

3.5. 오차가 미치는 영향

그림 2와 그림 4에서 그린 오차 범위 내에서 점들이 움직일 때, 그래프에 그려진 추세선의 기울기가 어떤 범위 내에서 움직이는지 확인하였다.

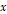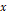점이 그림에서 표시된 오차 범위 내에서 움직였을 때 그래프에 그려진 추세선의 기울기가 최소가 되기 위해서는, 점들의 값이 10% 감소해야 하고, 값이 0.05 증가해야 하며, 기울기가 최대가 되기 위해서는 점들의 값이 10% 증가해야 하고, 값이 0.05 감소해야 한다. 이렇게 점들의 위치를 조정했을 때 그림 2와 그림 4가 어떻게 변화하는지 보았다.

그림 6 그림 2에 오차를 적용했을 때 추세선

그림 7 그림 3에 오차를 적용했을 때 추세선

위와 같이 모든 점들이 설명한 것과 같이 극단적인 오차를 가질 확률은 작으므로, 추세선이 위와 같이 극단적인 기울기를 가질 확률 또한 극도로 작다. 하지만 오차의 범위가 매우 넓으며 최대 최소 기울기의 차이가 꽤 큰 이유로 이 오차를 간단히 무시할 수는 없다. 물론 이 극단적인 기울기의 중간치 정도로 나온 이 실험 데이터의 정확도나 신뢰도가 훨씬 높다고 말할  수 있어 데이터의 신뢰도 자체는 높은 편이지만, 이런 오차 범위 또한 참고용으로 봐 두는 것이 좋을 것 같다는 결론을 내릴 수 있었다.

4. Conclusion

이 실험을 통해 전류와 전류 사이에 작용하는 자기장에 의한 힘을 확인해 보았다. 전류 천칭에 작용하는 자기장에 의한 힘이 만들어내는 돌림힘과 중력에 의해 만들어진 되돌림 돌림힘이 상쇄됨을 이용하여 이를 시행할 수 있었다.

이론에 의하면 천칭이 처음에 비해 각도 만큼 기울어졌을 때 값이 전류 천칭에 흐르는 전류 크기와 솔레노이드에 흐르는 전류 크기에 비례해야 한다. 첫 번째로, 솔레노이드에 흐르는 전류 크기가 일정할 때 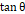의 값이 전류 천칭에 흐르는 전류 크기에 비례한지 확인하였다. 그래프를 그려 확인한 결과, 전체적인 관점에서 보았을 때 그 비례성을 찾아볼 수 있었다. 두 번째로, 전류 천칭에 흐르는 전류 크기가 일정할 때 값이 솔레노이드에 흐르는 전류의 크기에 비례한지 확인하였다. 그래프를 그려 확인한 결과, 마찬가지로 전체적인 관점에서 그 비례성을 찾아볼 수 있었다.

마지막으로 이론 값에 대한 정확도를 확인하였다. 실험 요건을 고려하여 계산했을 때, 이론대로라면 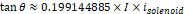라는 공식이 성립해야 하는데, 첫 번째와 두 번째 과정에서의 그래프에 그린 추세선의 기울기가 각각 솔레노이드, 전류 천칭에 흐르는 전류 크기에 따라 변하는 변화율이 와 같아야 한다. 실험을 통해 각각 얻어낸 값은 0.1954와 0.2016으로, 이론을 통해 얻어낸 값과 거의 일치함을 확인할 수 있었다.

하지만 분명히 이 실험에서 얻어낸 데이터에도 여러 가지 실험 요건으로 인해 발생한 오차가 존재했다. 전류 천칭의 흔들림이나 측정 한계 등을 그 원인으로 지목하였다. 더욱 더 이상적인 실험 요건을 위해서라면 우선 전류 천칭을 더욱 얇게 만들어야 하며, 받침대 못을 조금 더 두껍고 큰 것을 사용하고, 가리키개 변위 측정용 자의 눈금을 더욱 세밀하게 해야 한다. 전류 천칭의 흔들림을 감소시키기 위해서는 솔레노이드나 전류 천칭에 흘리는 전류의 크기를 너무 급격하게 바꾸지 않고 천천히 바꾸는 방법을 사용할 수 있다.

*Reference

1 서울대학교 물리천문학부, 『실험 2-3. 전류와 전류 사이』, 2017, 9