[서울대 물리학실험 1-6] 파동

물리학 실험 1-6

1-6. 파동

*본 보고서는 이미 제출된 보고서로 표절 시 발각될 확률이 높으니 참고만 해주시길 바랍니다.

1. Introduction

1.1. 실험 목적

수면파 발생 장치를 사용하여 결맞는 (coherent) 파동을 발생시키고, 그 진행 특성과 간섭 효과를 조사한다.

① 수면파의 발생 방법과 진행 과정, 전달 속력 등을 살펴본다.

② 두 개의 결맞는 점 파원으로부터의 수면파 간섭을 조사한다.

1.2. 배경 지식

1.2.1 파동에 대한 방정식

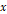+방향으로 진행하는 파동의 일반적 표현식은 시간 , 위치 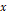에서의 진동 크기가 다음과 같다.

이때, 는 파동의 진폭, 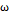는 각 진동수, 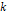는 파수이다. 이들은 다음과 같이 표현할 수 있다.

파동의 속력은 위상의 일정한 위치 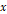가 시간 에 따라 변하는 율이다.

이것은 엄밀하게 말하면 파동의 위상 속도이다.

한편, 파동에 의해 정보를 전달하기 위해서는 일정한 진폭과 진동수의 단순 파동으로는 불가능하고, 여러 진동수의 단순 파동들이 중첩된 펄스와 같은 파동의 묶음이 필요하다. 이 묶음이 전달되는 속력을 군속력이라고 한다.

1.2.2 매질에 대하여

비분산매질 : , 즉 위상 속력이 진동수와 파장에 관계없이 일정한 매질이다. 여기서 다음이 성립함.

분산매질 : 위상 속력이 파장에 의존하는 매질이다.

1.2.3 파동의 간섭

진동수가 같으나 위상이 다른 두 결맞는 파가 있다.

이의 합성에 대해,

반사된 파와의 간섭을 생각하면,

이는 진행하지 않고 서 있는 파동, 정상파가 된다. 이 경우 인 곳은 마디, 인 곳은 배가 된다.

1.2.4 마디 배 판정

거리 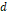만큼 떨어져 있는 두 결맞는 파원이 있다. 그림 1에서의 가 크지 않은 경우(보통 10도 아래), 두 파원을 점 파원으로 간주하면,

그림 1 두 파원으로부터의 영향

배가 생길 조건 :

마디가 생길 조건 :

1.2. 실험 안내

① 수조에 물을 2/3 가량 채운 뒤 수면파 발생 장치를 설치한다. 수조는 수평으로 놓고 수조의 가장자리에 스펀지로 수면파 흡수대를 놓는다. (반사파 방지용)

② I-CA를 켜고, 수면파 발생 장치 두 점의 거리를 실측해서 스케일을 정한다.

③ 조명의 주파수를 수면파의 주파수에 맞춘다.

④ 간섭 무늬가 가장 선명한 프레임에서 간접 지점을 찾아 각각 거리를 측정하여 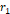, 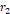를 측정한다.

⑤ 두 거리의 차가 정수배 관계인지 확인한다.

⑥ 측정값을 대입하여 를 구한다.

⑦ 거리 구하기 기능을 이용해 수면파의 속력을 측정한다. (그리드 보기를 통해 수면파의 한 점이 5~6 프레임 동안 얼마 이동했는지 측정)

⑧ 진동수를 변화시키고 실험을 더 한다.

2. Data & Result

2.1. 주파수가 14Hz인 물결파

파원이 되는 수면파 생성 장치 사이의 간격은 약 5cm였다.

그 다음, 파동의 위상 속도를 측정해보았다. 측정을 용이하게 하기 위해 파동의 간섭이 덜 일어나는 곳에서 속도를 측정하였다. 파동이 3.505cm를 움직이는데 0.233초가 걸렸으므로, 속도는 약 15.043cm/s이다. 물을 비분산매질로 간주한다면, 속도를 진동수로 나누어 파장 값을 구할 수 있을 것이다. 이렇게 해서 구한 14Hz 파동의 파장은 1.074cm, 16Hz 파동의 파장은 0.940cm이다.

간섭이 일어난 수면파 중 배에 해당하는 부분과 파원 사이의 거리를 각각 구했다. 아래 데이터는 14Hz 파동에 대한 것이며, 단위는 cm이다.

1	5.7	3.918	1.782
2	7.363	4.802	2.561
3	6.626	2.945	3.681

표 1 14Hz 파동의 거리 차

그리고 아래 데이터는 16Hz 파동에 대한 것이며, 단위는 cm이다.

1	4.759	2.906	1.853
2	6.754	4.121	2.633
3	6.830	3.289	3.541

표 2 16Hz 파동의 거리 차

이것이 실제로 정수배로 이루어지는지 확인하기 위해 우선 거리의 차에 대한 변화를 지켜보았다. 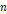이 1씩 증가할 때 증가하는 ‘파원으로부터의 거리의 차’ 값이 일정하면 일정할수록 거리의 차가 정수배로 이루어졌다고 말할 수가 있다. 다음은 이에 대해 조사한 결과이다.

	14Hz	16Hz
평균	1.227	1.853
표준편차	0.416404	0.47509

표 3 거리의 차 변화에 대한 조사

이 표에서 평균 값은 파동의 파장 값이 된다. 거리의 차에 파장 값을 나누었을 때 정수에 가깝게 나온다면 파원으로부터의 거리의 차가 정수배로 이루어진다고 말할 수 있을 것이다. 위의 평균 값을 파장으로 간주하고 그래프를 그린 다음, 그 그래프와 선 사이에 얼마나 차이가 있는지 살펴 보았다.

그림 2 정수배인지 비교하는 그래프

이 그래프는 그 거리의 차가 정수배라고 설정한 귀무(歸無)가 참이라는 가정 하에 그려진 것이다. 더 다양한 관점에서 바라보기 위해 실측한 파장을 이용하여 그래프를 그리기로 하였다. 파동의 간섭이 덜 미치는 부분, 즉 파원과 거리가 먼 부분에서 파장을 실측했을 때에는, 14Hz 파동의 경우 1.404cm, 16Hz 파동의 경우 1.184cm이 파장 값으로 나왔다. 이를 이용하여 그래프를 그리면 다음과 같이 나온다.

그림 3 정수배인지 비교하는 그래프 2

3. Discussion

데이터에 영향을 미치거나, 혹은 데이터를 오염시켰을 수 있는 요소들은 다음과 같다.

3.1. 기계 오류

기계의 수면파 생성 장치가 서로 동일하게 움직여야 하는데 각각 다르게 움직이는 것을 확연히 볼 수 있었다. 나사를 조절하여 이를 최대한 억제하려고 했으나, 이 기계 오류가 데이터에 영향을 미쳤을 가능성이 있다고 볼 수 있다.

3.2. 수조의 수평 문제

수조가 실제로는 수평을 이루지 않아서 데이터에 오류를 일으켰을 가능성이 있다.

3.3. 물과 수조의 마찰 등등

바닥 쪽의 물과 수조 사이의 마찰과 같이 파동 에너지의 감소에 영향을 줄 수 있는 힘이 데이터에 영향을 미쳤을 가능성이 상당히 있다. 수조 내에서 파동의 모습이 파원에서 멀어질수록 어느 정도 희미해진 것을 보았을 때 이와 같은 힘이 무시할 정도는 아니라고 생각을 하였다.

3.4. 평행광

광원이 완벽한 평행광이 아니어서 관측한 파장 값과 실제 파장 값이 다르는 등 결과에 왜곡을 줄 수 있다.

3.5. 구슬이 점 파원이라 하기에는 큼

파원으로부터 배 사이의 거리를 측정할 때에는 구슬이 점에 가깝다고 보고 구슬의 중심과 배 사이의 거리를 측정하였다. 하지만, 실제로 구슬은 조금 큰 편이었고, 이 요인이 데이터에 영향을 끼칠 수 있을 것이라고 판단하였다.

4. Conclusion

배 부분에서 두 파원으로부터 거리의 차가 파장의 정수배를 이루는지 확인해보았다. 이를 위해서는 우선 파장을 먼저 알고 있어야 했다.

처음에는 속도를 이용하여 파장을 구했다. 그 다음에는 거리의 차의 평균 변화량을 이용해서, 그리고 마지막으로는 실측 값을 이용하여 파장을 구했다. 각각의 값마다 어느 정도 차이가 있었고, 특히 14Hz 파동의 경우에는 더욱 그랬다. 이 중에서 속도를 이용하여 구한 파장 값이 가장 괴리가 있었는데, 이의 원인으로는 물과 수조의 마찰 문제를 생각할 수 있었다. 파동의 위상 속도를 측정한 곳이 파원으로부터 상대적으로 거리가 먼 곳이었는데, 파동이 물과 수조 사이의 마찰력 때문에 파동 에너지를 일정 부분 잃었을 가능성을 생각할 수 있었다.

파장을 구하고 나서는 두 파원으로부터의 거리의 차를 파장으로 나눈 값이 정수에 가까운지 확인하였다. 거리의 차가 작은 경우에는 정수에서 벗어나는 모습을 보이기도 하였으나, 거리의 차가 크면 클수록 정수에 가까워지는 모습을 보였다. 이의 이유로는 구슬이 점 파원이라 하기에는 너무 컸다는 점을 꼽을 수 있었다. 거리가 멀다면 구슬 크기의 영향이 완화될 수 있지만, 거리가 가까운 경우에는 파원으로부터의 거리 측정 시 구슬의 크기가 영향을 줄 수 있기 때문이다.

이 말고도 이론과 차이를 보이는 이유에 대해서 여러 가지를 꼽을 수 있었다. 가장 먼저, 기계의 오작동을 꼽을 수 있었다. 파동을 생성하는 장치는 동일하게 움직이는 것이 정상이나, 장치가 실험 도중 따로따로 움직이는 모습을 관찰할 수 있었으며, 이것이 실험 결과에 영향을 미쳤을 가능성이 있다고 판단하였다. 또 물과 수조 사이의 마찰이나 수조의 평형 여부 문제가 실험 결과에 영향을 미쳤을 가능성이 있다고 판단하였다.

다음과 같은 요인들이나 구슬의 크기를 고려했을 때, 파원으로부터 거리가 먼 부분에서는 파원으로부터의 거리 차가 정수배인 모습을 보이는 것을 보아, 파원으로부터의 거리 차가 정수배라는 것을 일정 부분 확인할 수 있었다고 판단을 내릴 수 있었다.

*Reference

1 서울대학교 물리천문학부, 『실험 1-6. 파동』, 2015, 10